Chapter 5. Requêtes spatiales

Selon le OpenGIS Simple Features Implementation Specification for SQL, "l'approche de base pour comparer deux géométries consiste à effectuer des tests par paire des intersections entre les intérieurs, les limites et les extérieurs des deux géométries et à classer la relation entre les deux géométries sur la base des entrées de la matrice "intersection" résultante."

Dans la théorie de la topologie des ensembles de points, les points d'une géométrie intégrée dans un espace à deux dimensions sont classés en trois ensembles :

Le Dimensionally Extended 9-Intersection Model (DE-9IM) décrit la relation spatiale entre deux géométries en spécifiant les dimensions des 9 intersections entre les ensembles ci-dessus pour chaque géométrie. Les dimensions des intersections peuvent être représentées formellement dans une matrice d'intersections de 3x3.

Pour une géométrie g, les Limites, Intérieures, et Extérieures sont désignés par la notation I(g), B(g), et E(g). En outre, dim(s) désigne la dimension d'un ensemble s dont le domaine est {0,1,2,F} :

En utilisant cette notation, la matrice d'intersection pour deux géométries a et b est :

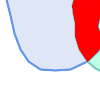
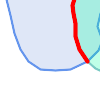
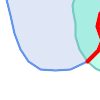
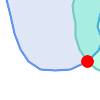
Visuellement, pour deux géométries polygonales qui se chevauchent, cela ressemble à ce qui suit :

	Intérieur Limite Extérieur Intérieur dim( I(a) ∩ I(b) ) = 2 dim( I(a) ∩ B(b) = 1 dim( I(a) ∩ E(b) ) = 2 Limite dim( B(a) ∩ I(b) ) = 1 dim( B(a) ∩ B(b) ) = 0 dim( B(a) ∩ E(b) ) = 1 Extérieur dim( E(a) ∩ I(b) ) = 2 dim( E(a) ∩ B(b) ) = 1 dim( E(a) ∩ E(b) = 2

En lisant de gauche à droite et de haut en bas, la matrice d'intersection est représentée par la chaîne de texte "212101212".

Pour plus d'informations, voir :

Pour faciliter la détermination des relations spatiales communes, l'OGC SFS définit un ensemble de prédicats de relations spatiales. PostGIS fournit ces prédicats sous la forme des fonctions ST_Contains, ST_Crosses, ST_Disjoint, ST_Equals, ST_Intersects, ST_Overlaps, ST_Touches, ST_Within. Il définit également les prédicats de relation non standard ST_Covers, ST_CoveredBy, et ST_ContainsProperly.

Les prédicats spatiaux sont généralement utilisés comme conditions dans les clauses SQL WHERE ou JOIN. Les prédicats spatiaux nommés utilisent automatiquement un index spatial s'il existe, de sorte qu'il n'est pas nécessaire d'utiliser également l'opérateur de boîte de délimitation &&. Par exemple :

SELECT city.name, state.name, city.geom
FROM city JOIN state ON ST_Intersects(city.geom, state.geom);

Pour plus de détails et d'illustrations, voir l' Atelier PostGIS.

Dans certains cas, les relations spatiales nommées sont insuffisantes pour fournir une condition de filtrage spatial souhaitée.

Prenons l'exemple d'un ensemble de données linéaires représentant un réseau routier. Il peut être nécessaire d'identifier tous les segments de route qui se croisent, non pas en un point, mais en une ligne (peut-être pour valider une règle commerciale). Dans ce cas, ST_Crosses ne fournit pas le filtre spatial nécessaire, puisque pour les caractéristiques linéaires, il renvoie true uniquement lorsqu'elles se croisent en un point. Une solution en deux étapes consisterait à calculer d'abord l'intersection réelle (ST_Intersection) des paires de lignes routières qui se croisent dans l'espace (ST_Intersects), puis vérifier si le ST_GeometryType de l'intersection est "LINESTRING" (en traitant correctement les cas qui renvoient des GEOMETRYCOLLECTIONs de [MULTI]POINTs, [MULTI]LINESTRINGs, etc. ). Il est évident qu'une solution plus simple et plus rapide est souhaitable.

Un deuxième exemple est la localisation des quais qui coupent les limites d'un lac sur une ligne et dont l'une des extrémités se trouve sur le rivage. En d'autres termes, lorsqu'un quai est situé à l'intérieur d'un lac mais n'est pas complètement contenu par celui-ci, qu'il coupe la limite d'un lac sur une ligne et que l'une des extrémités du quai se trouve à l'intérieur ou sur la limite du lac. Il est possible d'utiliser une combinaison de prédicats spatiaux pour trouver les caractéristiques requises : ST_Contains(lake, wharf) = TRUE ST_ContainsProperly(lake, wharf) = FALSE ST_GeometryType(ST_Intersection(wharf, lake)) = 'LINESTRING' ST_NumGeometries(ST_Multi(ST_Intersection(ST_Boundary(wharf), ST_Boundary(lake)))) = 1 ... mais inutile de dire que c'est assez compliqué.

Ces exigences peuvent être satisfaites en calculant la matrice d'intersection DE-9IM complète. PostGIS fournit la fonction ST_Relate pour ce faire :

SELECT ST_Relate( 'LINESTRING (1 1, 5 5)',
                  'POLYGON ((3 3, 3 7, 7 7, 7 3, 3 3))' );
st_relate
-----------
1010F0212

Pour tester une relation spatiale particulière, un modèle de matrice d'intersection est utilisé. Il s'agit de la représentation matricielle augmentée des symboles supplémentaires {T,*} :

Les modèles de matrice d'intersection permettent d'évaluer des relations spatiales spécifiques de manière plus succincte. Les fonctions ST_Relate et ST_RelateMatch peuvent être utilisées pour tester les modèles de matrice d'intersection. Pour le premier exemple ci-dessus, le modèle de matrice d'intersection spécifiant deux lignes se croisant dans une ligne est '1*1***1**' :

-- Find road segments that intersect in a line
SELECT a.id
FROM roads a, roads b
WHERE a.id != b.id
      AND a.geom && b.geom
      AND ST_Relate(a.geom, b.geom, '1*1***1**');

Pour le deuxième exemple, le modèle de matrice d'intersection spécifiant une ligne située en partie à l'intérieur et en partie à l'extérieur d'un polygone est "102101FF2" :

-- Find wharves partly on a lake's shoreline
SELECT a.lake_id, b.wharf_id
FROM lakes a, wharfs b
WHERE a.geom && b.geom
      AND ST_Relate(a.geom, b.geom, '102101FF2');