ST_DelaunayTriangles

ST_DelaunayTriangles
Prev	7.14. Geometrieverarbeitung	Next

Name

ST_DelaunayTriangles — Returns the Delaunay triangulation of the vertices of a geometry.

Synopsis

geometry ST_DelaunayTriangles(geometry g1, float tolerance = 0.0, int4 flags = 0);

Beschreibung

Computes the Delaunay triangulation of the vertices of the input geometry. The optional tolerance can be used to snap nearby input vertices together, which improves robustness in some situations. The result geometry is bounded by the convex hull of the input vertices. The result geometry representation is determined by the flags code:

0 - a GEOMETRYCOLLECTION of triangular POLYGONs (default)
1 - a MULTILINESTRING of the edges of the triangulation
2 - A TIN of the triangulation

Wird vom GEOS Modul ausgeführt

Verfügbarkeit: 2.1.0

This function supports 3d and will not drop the z-index.

This function supports Triangles and Triangulated Irregular Network Surfaces (TIN).

Beispiele

Ursprüngliche Polygone

our original geometry
    ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        )

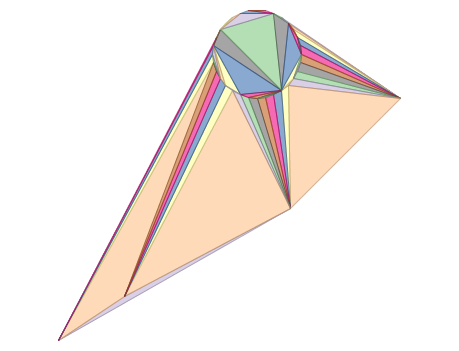ST_DelaunayTriangles von 2 Polygonen: delaunay triangulierte Polygone, jedes der Dreiecke ist in einer eigenen Farbe dargestellt


geometries overlaid multilinestring triangles

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ))
     As  dtriag;

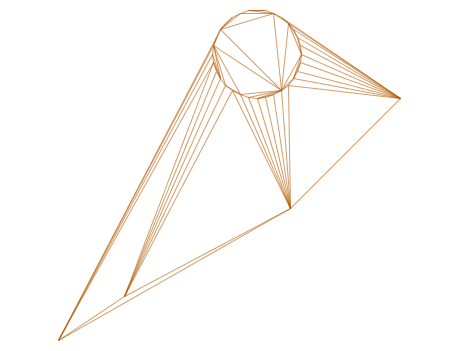-- Delaunay-Dreiecke als MultiLinestring

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ),0.001,1)
     As  dtriag;

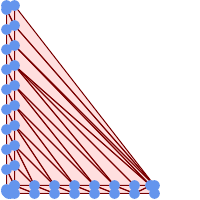-- Delaunay Dreiecke von 45 Punkten als 55 Dreieckspolygone


this produces a table of 42 points that form an L shape

SELECT (ST_DumpPoints(ST_GeomFromText(
'MULTIPOINT(14 14,34 14,54 14,74 14,94 14,114 14,134 14,
150 14,154 14,154 6,134 6,114 6,94 6,74 6,54 6,34 6,
14 6,10 6,8 6,7 7,6 8,6 10,6 30,6 50,6 70,6 90,6 110,6 130,
6 150,6 170,6 190,6 194,14 194,14 174,14 154,14 134,14 114,
14 94,14 74,14 54,14 34,14 14)'))).geom
    INTO TABLE l_shape;

output as individual polygon triangles

SELECT ST_AsText((ST_Dump(geom)).geom) As wkt
FROM ( SELECT ST_DelaunayTriangles(ST_Collect(geom)) As geom
FROM l_shape) As foo;


wkt

POLYGON((6 194,6 190,14 194,6 194))
POLYGON((14 194,6 190,14 174,14 194))
POLYGON((14 194,14 174,154 14,14 194))
POLYGON((154 14,14 174,14 154,154 14))
POLYGON((154 14,14 154,150 14,154 14))
POLYGON((154 14,150 14,154 6,154 14))

Example using vertices with Z values.


3D multipoint

SELECT ST_AsText(ST_DelaunayTriangles(ST_GeomFromText(
         'MULTIPOINT Z(14 14 10, 150 14 100,34 6 25, 20 10 150)'))) As wkt;


wkt

GEOMETRYCOLLECTION Z (POLYGON Z ((14 14 10,20 10 150,34 6 25,14 14 10))
 ,POLYGON Z ((14 14 10,34 6 25,150 14 100,14 14 10)))

Siehe auch

ST_VoronoiPolygons, ST_TriangulatePolygon, ST_ConstrainedDelaunayTriangles, ST_VoronoiLines, ST_ConvexHull