26. Modelo de intersección 9 dimensionalmente extendido(DE-9IM)

El «Dimensionally Extended 9-Intersection Model <http://en.wikipedia.org/wiki/DE-9IM>» (DE9IM) es un marco para modelar cómo interactúan dos objetos espaciales.

Primero, cada objeto espacial tiene:

• Un interior

• Un límite

• Un exterior

Para polígonos, el interior, límite y exterior son obvios:

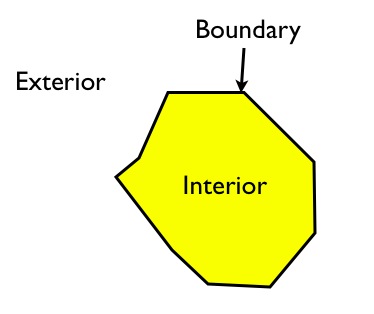
El interior es la parte delimitada por los anillos; el límite son los anillos mismos; el exterior es todo lo demás en el plano.

Para elementos lineales, el interior, límite y exterior son menos conocidos:

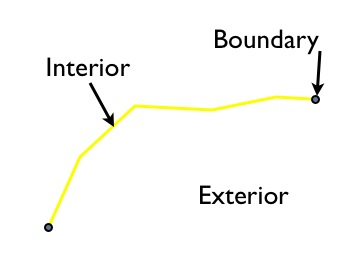
El interior es la parte de la línea delimitada por los extremos; el límite son los extremos de la línea, y el exterior es todo lo demás en el plano.

Para puntos, las cosas son aún más extrañas: el interior es el punto; el límite es el conjunto vacío y el exterior es todo lo demás en el plano.

Usando estas definiciones de interior, exterior y límite, las relaciones entre cualquier par de objetos espaciales pueden caracterizarse usando la dimensionalidad de las nueve posibles intersecciones entre los interiores/límites/exteriores de un par de objetos.

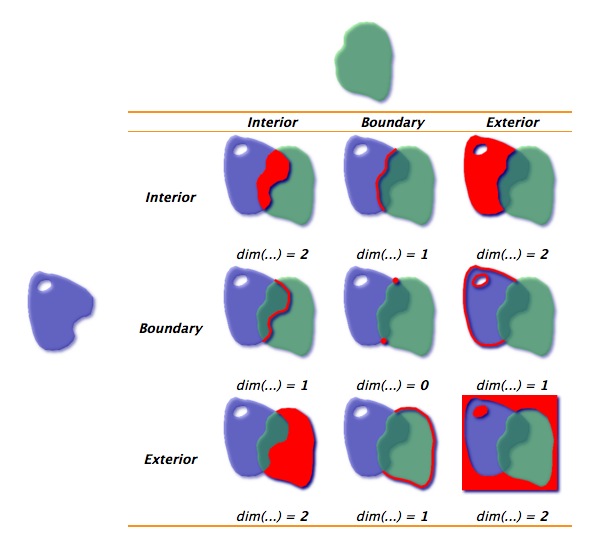
Para los polígonos en el ejemplo anterior, la intersección de los interiores es un área bidimensional, por lo que esa parte de la matriz se completa con un «2». Los límites solo se intersectan en puntos, que son de dimensión cero, por lo que esa parte de la matriz se completa con un 0.

Cuando no hay intersección entre componentes, el cuadro de la matriz se completa con una «F».

Aquí hay otro ejemplo, de una línea que entra parcialmente en un polígono:

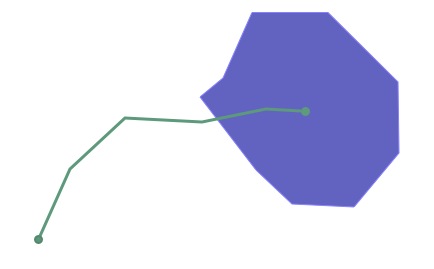
La matriz DE9IM para la interacción es esta:

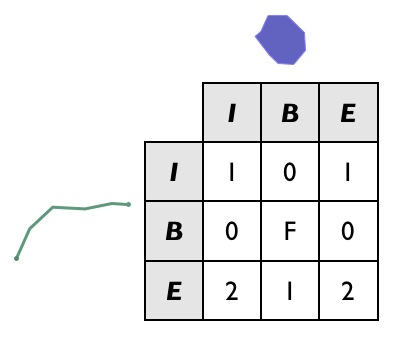
Observa que los límites de los dos objetos en realidad no se intersectan en absoluto (el extremo de la línea interactúa con el interior del polígono, no con el límite, y viceversa), por lo que la celda B/B se completa con una «F».

Aunque es divertido completar matrices DE9IM visualmente, sería mejor si una computadora pudiera hacerlo, y para eso sirve la función ST_Relate.

El ejemplo anterior puede simplificarse usando una simple caja y línea, con la misma relación espacial que nuestro polígono y línea:

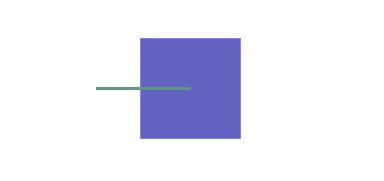
Y podemos generar la información DE9IM en SQL:

SELECT ST_Relate(
         'LINESTRING(0 0, 2 0)',
         'POLYGON((1 -1, 1 1, 3 1, 3 -1, 1 -1))'
       );

La respuesta (1010F0212) es la misma que calculamos visualmente, pero devuelta como una cadena de 9 caracteres, con la primera fila, segunda fila y tercera fila de la tabla concatenadas.

101
0F0
212

Sin embargo, el poder de las matrices DE9IM no está en generarlas, sino en usarlas como clave de coincidencia para encontrar geometrías con relaciones muy específicas entre sí.

CREATE TABLE lakes ( id serial primary key, geom geometry );
CREATE TABLE docks ( id serial primary key, good boolean, geom geometry );

INSERT INTO lakes ( geom )
  VALUES ( 'POLYGON ((100 200, 140 230, 180 310, 280 310, 390 270, 400 210, 320 140, 215 141, 150 170, 100 200))');

INSERT INTO docks ( geom, good )
  VALUES
        ('LINESTRING (170 290, 205 272)',true),
        ('LINESTRING (120 215, 176 197)',true),
        ('LINESTRING (290 260, 340 250)',false),
        ('LINESTRING (350 300, 400 320)',false),
        ('LINESTRING (370 230, 420 240)',false),
        ('LINESTRING (370 180, 390 160)',false);

Supongamos que tenemos un modelo de datos que incluye Lagos y Muelles, y supongamos además que los muelles deben estar dentro de los lagos, y deben tocar el límite de su lago contenedor en un extremo. ¿Podemos encontrar todos los muelles en nuestra base de datos que obedezcan esa regla?

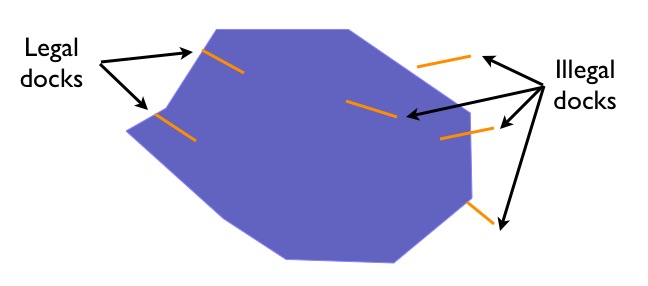
Nuestros muelles legales tienen las siguientes características:

• Sus interiores tienen una intersección lineal (1D) con el interior del lago

• Sus límites tienen una intersección puntual (0D) con el interior del lago

• Sus límites también tienen una intersección puntual (0D) con el límite del lago

• Sus interiores no tienen intersección (F) con el exterior del lago

Así que su matriz DE9IM se ve así:

Entonces, para encontrar todos los muelles legales, queremos encontrar todos los muelles que intersecten lagos (un superconjunto de candidatos potenciales que usamos como clave de unión), y luego encontrar todos los muelles en ese conjunto que tengan el patrón legal de relación.

SELECT docks.*
FROM docks JOIN lakes ON ST_Intersects(docks.geom, lakes.geom)
WHERE ST_Relate(docks.geom, lakes.geom, '1FF00F212');

-- Answer: our two good docks

Observa el uso de la versión de tres parámetros de ST_Relate, que devuelve verdadero si el patrón coincide o falso si no lo hace. Para un patrón completamente definido como este, la versión de tres parámetros no es necesaria: podríamos haber usado simplemente un operador de igualdad de cadena.

Sin embargo, para búsquedas de patrones más flexibles, la de tres parámetros permite caracteres de sustitución en la cadena de patrón:

• «*» significa «cualquier valor en esta celda es aceptable»

• «T» significa «cualquier valor no falso (0, 1 o 2) es aceptable»

Así que, por ejemplo, un muelle posible que no incluimos en nuestro gráfico de ejemplo es un muelle con una intersección bidimensional con el límite del lago:

INSERT INTO docks ( geom, good )
  VALUES ('LINESTRING (140 230, 150 250, 210 230)',true);

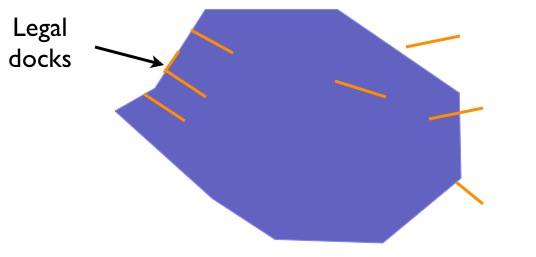
Si vamos a incluir este caso en nuestro conjunto de muelles «legales», necesitamos cambiar el patrón de relación en nuestra consulta. En particular, la intersección del interior del muelle con el límite del lago ahora puede ser 1 (nuestro nuevo caso) o F (nuestro caso original). Así que usamos el comodín «*» en el patrón.

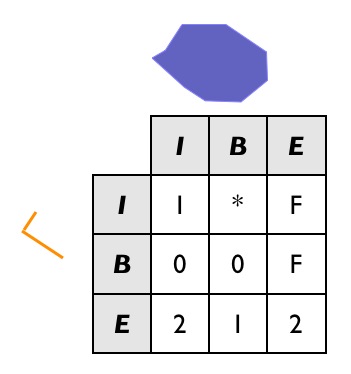
Y el SQL se ve así:

SELECT docks.*
FROM docks JOIN lakes ON ST_Intersects(docks.geom, lakes.geom)
WHERE ST_Relate(docks.geom, lakes.geom, '1*F00F212');

-- Answer: our (now) three good docks

Confirma que el SQL más estricto del ejemplo anterior no devuelve el nuevo muelle.

26.1. Pruebas de Calidad de Datos

Los datos TIGER se controlan cuidadosamente en cuanto a calidad cuando se preparan, por lo que esperamos que nuestros datos cumplan normas estrictas. Por ejemplo: ningún bloque censal debería superponerse con otro bloque censal. ¿Podemos probar eso?

¡Claro!

SELECT a.gid, b.gid
FROM nyc_census_blocks a, nyc_census_blocks b
WHERE ST_Intersects(a.geom, b.geom)
  AND ST_Relate(a.geom, b.geom, '2********')
  AND a.gid != b.gid
LIMIT 10;

-- Answer: 10, there's some funny business

De manera similar, esperaríamos que los datos de carreteras estén todos correctamente nodificados en los extremos. Es decir, esperamos que las intersecciones solo ocurran en los extremos de las líneas, no en los puntos medios.

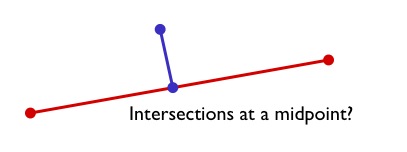
Podemos probar eso buscando calles que se intersecten (de modo que tengamos una unión) pero donde la intersección entre los límites no sea de dimensión cero (es decir, los extremos no se tocan):

SELECT a.gid, b.gid
FROM nyc_streets a, nyc_streets b
WHERE ST_Intersects(a.geom, b.geom)
  AND NOT ST_Relate(a.geom, b.geom, '****0****')
  AND a.gid != b.gid
LIMIT 10;

-- Answer: This happens, so the data is not end-noded.

26.1.1. Lista de funciones

ST_Relate(geometry A, geometry B) <http://postgis.net/docs/ST_Relate.html>: Devuelve una cadena de texto que representa la relación DE9IM entre las geometrías.