Name
ST_HexagonGrid — Returns a set of hexagons and cell indices that completely cover the bounds of the geometry argument.
Synopsis
setof record ST_HexagonGrid(float8 size, geometry bounds);
Description
Starts with the concept of a hexagon tiling of the plane. (Not a hexagon tiling of the globe, this is not the H3 tiling scheme.) For a given planar SRS, and a given edge size, starting at the origin of the SRS, there is one unique hexagonal tiling of the plane, Tiling(SRS, Size). This function answers the question: what hexagons in a given Tiling(SRS, Size) overlap with a given bounds.
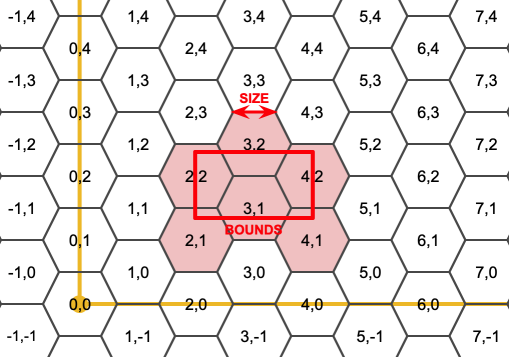
The SRS for the output hexagons is the SRS provided by the bounds geometry.
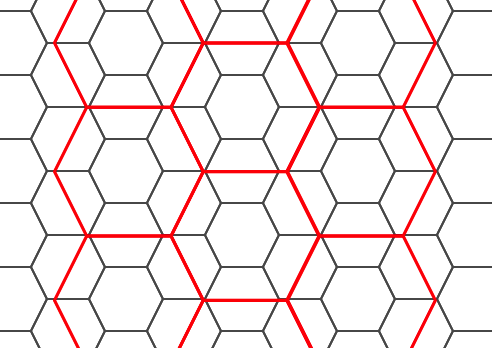
Doubling or tripling the edge size of the hexagon generates a new parent tiling that fits with the origin tiling. Unfortunately, it is not possible to generate parent hexagon tilings that the child tiles perfectly fit inside.
Availability: 3.1.0
Example: Counting points in hexagons
To do a point summary against a hexagonal tiling, generate a hexagon grid using the extent of the points as the bounds, then spatially join to that grid.
SELECT COUNT(*), hexes.geom
FROM
ST_HexagonGrid(
10000,
ST_SetSRID(ST_EstimatedExtent('pointtable', 'geom'), 3857)
) AS hexes
INNER JOIN
pointtable AS pts
ON ST_Intersects(pts.geom, hexes.geom)
GROUP BY hexes.geom;
Example: Generating hex coverage of polygons
If we generate a set of hexagons for each polygon boundary and filter out those that do not intersect their hexagons, we end up with a tiling for each polygon.
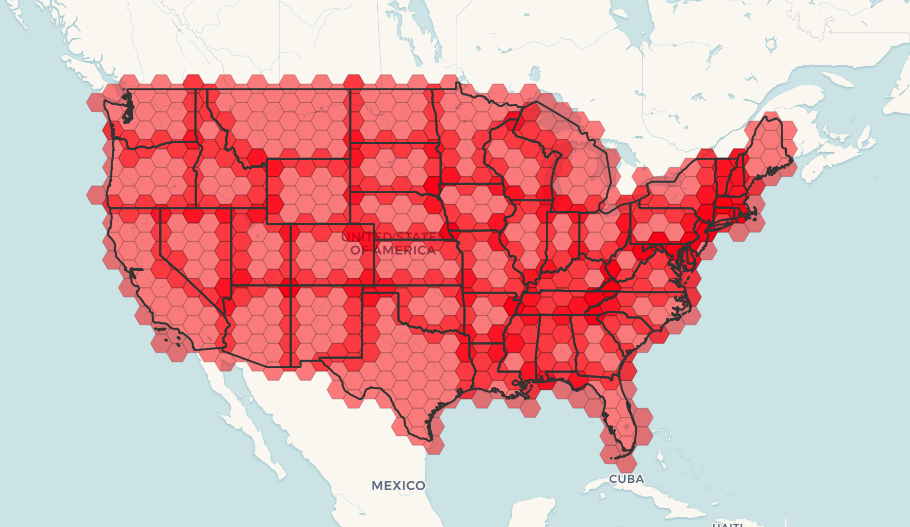
Tiling states results in a hexagon coverage of each state, and multiple hexagons overlapping at the borders between states.
![[Note]](../images/note.png)
|
|
|
The LATERAL keyword is implied for set-returning functions when referring to a prior table in the FROM list. So CROSS JOIN LATERAL, CROSS JOIN, or just plain , are equivalent constructs for this example. |
SELECT admin1.gid, hex.geom
FROM
admin1
CROSS JOIN
ST_HexagonGrid(100000, admin1.geom) AS hex
WHERE
adm0_a3 = 'USA'
AND
ST_Intersects(admin1.geom, hex.geom)
See Also
ST_EstimatedExtent, ST_SetSRID, ST_SquareGrid, ST_TileEnvelope