Name
CG_Tesselate — 对多边形或多面体表面执行曲面细分,并以 TIN 或 TINS 集合的形式返回
Synopsis
geometry CG_Tesselate(geometry geom);
描述
将 MULTI(POLYGON) 或 POLYHEDRALSURFACE 等曲面作为输入,并通过使用三角形的细分过程返回 TIN 表示形式。
![[Note]](../images/note.png)
|
|
|
ST_TriangulatePolygon 与此函数类似,但返回一个多边形的几何集合而不是三角形网,并且仅适用于二维几何。 |
可用性:3.5.0
 该方法需要SFCGAL后端。
该方法需要SFCGAL后端。
 该函数支持 3d 并且不会丢失 z-index。
该函数支持 3d 并且不会丢失 z-index。
 该函数支持多面体曲面。
该函数支持多面体曲面。
 此函数支持三角形和不规则三角网面 (TIN)。
此函数支持三角形和不规则三角网面 (TIN)。
示例
SELECT ST_GeomFromText('POLYHEDRALSURFACE Z( ((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)),
((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)), ((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),
((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)),
((0 1 0, 0 1 1, 1 1 1, 1 1 0, 0 1 0)), ((0 0 1, 1 0 1, 1 1 1, 0 1 1, 0 0 1)) )');
 原始立方体 |
SELECT CG_Tesselate(ST_GeomFromText('POLYHEDRALSURFACE Z( ((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)),
((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)), ((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),
((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)),
((0 1 0, 0 1 1, 1 1 1, 1 1 0, 0 1 0)), ((0 0 1, 1 0 1, 1 1 1, 0 1 1, 0 0 1)) )'));
ST_AsText 输出: TIN Z (((0 0 0,0 0 1,0 1 1,0 0 0)),((0 1 0,0 0 0,0 1 1,0 1 0)),
((0 0 0,0 1 0,1 1 0,0 0 0)),
((1 0 0,0 0 0,1 1 0,1 0 0)),((0 0 1,1 0 0,1 0 1,0 0 1)),
((0 0 1,0 0 0,1 0 0,0 0 1)),
((1 1 0,1 1 1,1 0 1,1 1 0)),((1 0 0,1 1 0,1 0 1,1 0 0)),
((0 1 0,0 1 1,1 1 1,0 1 0)),((1 1 0,0 1 0,1 1 1,1 1 0)),
((0 1 1,1 0 1,1 1 1,0 1 1)),((0 1 1,0 0 1,1 0 1,0 1 1)))
 带有彩色三角形的细分立方体 |
SELECT 'POLYGON (( 10 190, 10 70, 80 70, 80 130, 50 160, 120 160, 120 190, 10 190 ))'::geometry;
 原始多边形 |
SELECT
CG_Tesselate('POLYGON (( 10 190, 10 70, 80 70, 80 130, 50 160, 120 160, 120 190, 10 190 ))'::geometry);
ST_AsText 输出 TIN(((80 130,50 160,80 70,80 130)),((50 160,10 190,10 70,50 160)),
((80 70,50 160,10 70,80 70)),((120 160,120 190,50 160,120 160)),
((120 190,10 190,50 160,120 190)))
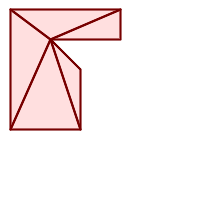 细分多边形 |