ST_DelaunayTriangles

ST_DelaunayTriangles
Prev	7.14. Traitement des géométries	Next

Name

ST_DelaunayTriangles — Renvoie la triangulation de Delaunay des sommets d'une géométrie.

Synopsis

geometry ST_DelaunayTriangles(geometry g1, float tolerance = 0.0, int4 flags = 0);

Description

Calcule la Delaunay triangulation des sommets de la géométrie d'entrée. La tolerance optionnelle peut être utilisée pour regrouper les sommets proches, ce qui améliore la robustesse dans certaines situations. La géométrie résultante est délimitée par l'enveloppe convexe des sommets de la géométrie d'entrée. La représentation de la géométrie résultante est déterminée par le code flags :

0 - une collection de géométries de POLYGONES triangulaires (par défaut)
1 - une MULTILINESTRING des arêtes de la triangulation
2 - Un TIN de la triangulation

Effectué par le module GEOS.

Disponibilité : 2.1.0

Cette fonction prend en charge la 3D et ne supprime pas l'indice z.

Cette fonction prend en charge les triangles et les réseaux irréguliers triangulés (TIN).

Exemples

Polygones d'origine

our original geometry
    ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        )

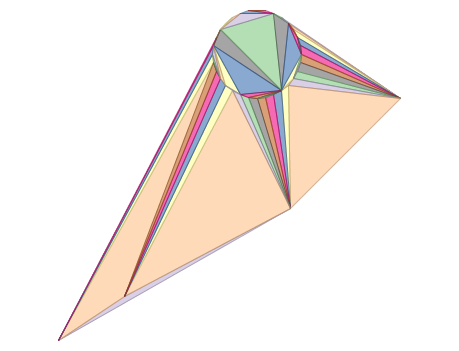ST_DelaunayTriangles de 2 polygones : polygones de triangle delaunay, chaque triangle est thématisé dans une couleur différente


geometries overlaid multilinestring triangles

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ))
     As  dtriag;

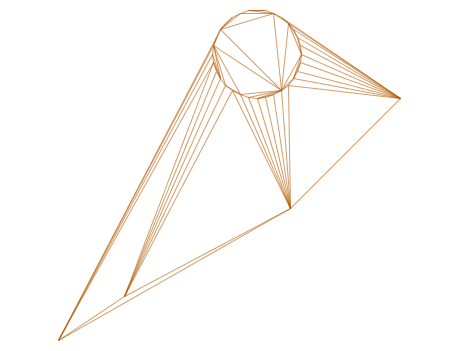-- triangles de delaunay en tant que multilignes

SELECT
    ST_DelaunayTriangles(
        ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
            50 60, 125 100, 175 150))'),
        ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
        ),0.001,1)
     As  dtriag;

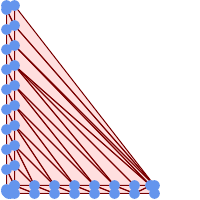-- triangles de delaunay de 45 points sous forme de 55 polygones triangulaires


this produces a table of 42 points that form an L shape

SELECT (ST_DumpPoints(ST_GeomFromText(
'MULTIPOINT(14 14,34 14,54 14,74 14,94 14,114 14,134 14,
150 14,154 14,154 6,134 6,114 6,94 6,74 6,54 6,34 6,
14 6,10 6,8 6,7 7,6 8,6 10,6 30,6 50,6 70,6 90,6 110,6 130,
6 150,6 170,6 190,6 194,14 194,14 174,14 154,14 134,14 114,
14 94,14 74,14 54,14 34,14 14)'))).geom
    INTO TABLE l_shape;

output as individual polygon triangles

SELECT ST_AsText((ST_Dump(geom)).geom) As wkt
FROM ( SELECT ST_DelaunayTriangles(ST_Collect(geom)) As geom
FROM l_shape) As foo;


wkt

POLYGON((6 194,6 190,14 194,6 194))
POLYGON((14 194,6 190,14 174,14 194))
POLYGON((14 194,14 174,154 14,14 194))
POLYGON((154 14,14 174,14 154,154 14))
POLYGON((154 14,14 154,150 14,154 14))
POLYGON((154 14,150 14,154 6,154 14))

Exemple utilisant des sommets avec des valeurs Z.


3D multipoint

SELECT ST_AsText(ST_DelaunayTriangles(ST_GeomFromText(
         'MULTIPOINT Z(14 14 10, 150 14 100,34 6 25, 20 10 150)'))) As wkt;


wkt

GEOMETRYCOLLECTION Z (POLYGON Z ((14 14 10,20 10 150,34 6 25,14 14 10))
 ,POLYGON Z ((14 14 10,34 6 25,150 14 100,14 14 10)))

Voir aussi

ST_VoronoiPolygons, ST_TriangulatePolygon, ST_ConstrainedDelaunayTriangles, ST_VoronoiLines, ST_ConvexHull