lw_dist2d_arc_arc()

int lw_dist2d_arc_arc	(	const POINT2D *	A1,
		const POINT2D *	A2,
		const POINT2D *	A3,
		const POINT2D *	B1,
		const POINT2D *	B2,
		const POINT2D *	B3,
		DISTPTS *	dl
	)

Definition at line 1687 of file measures.c.

{
        POINT2D pts_A[16];            /* Points on A that might be the nearest */
        POINT2D pts_B[16];            /* Points on B that might be the nearest */
        uint32_t ai = 0, bi = 0;      /* Number of points in pts_A and pts_B */
        POINT2D center_A, center_B;   /* Center points of arcs A and B */
        double radius_A, radius_B, d; /* Radii of arcs A and B */
        int is_disjoint, is_overlapping, is_contained, is_same_center;
        POINT2D intersectionPts[2];
 
        if (dl->mode != DIST_MIN)
                lwerror("lw_dist2d_arc_arc only supports mindistance");
 
        /* What if one or both of our "arcs" is actually a point? */
        if (lw_arc_is_pt(B1, B2, B3) && lw_arc_is_pt(A1, A2, A3))
                return lw_dist2d_pt_pt(B1, A1, dl);
        else if (lw_arc_is_pt(B1, B2, B3))
                return lw_dist2d_pt_arc(B1, A1, A2, A3, dl);
        else if (lw_arc_is_pt(A1, A2, A3))
                return lw_dist2d_pt_arc(A1, B1, B2, B3, dl);
 
        /* Calculate centers and radii of circles. */
        radius_A = lw_arc_center(A1, A2, A3, &center_A);
        radius_B = lw_arc_center(B1, B2, B3, &center_B);
 
        /* Two co-linear arcs?!? That's two segments. */
        if (radius_A < 0 && radius_B < 0)
                return lw_dist2d_seg_seg(A1, A3, B1, B3, dl);
 
        /* A is co-linear, delegate to lw_dist_seg_arc here. */
        if (radius_A < 0)
                return lw_dist2d_seg_arc(A1, A3, B1, B2, B3, dl);
 
        /* B is co-linear, delegate to lw_dist_seg_arc here. */
        if (radius_B < 0)
                return lw_dist2d_seg_arc(B1, B3, A1, A2, A3, dl);
 
        /* Circle relationships */
        d = distance2d_pt_pt(&center_A, &center_B);
        is_disjoint = (d > (radius_A + radius_B));
        is_contained = (d < fabs(radius_A - radius_B));
        is_same_center = p2d_same(&center_A, &center_B);
        is_overlapping = ! (is_disjoint || is_contained || is_same_center);
 
        /*
         * Prime the array of potential closest points with the
         * arc end points, which frequently participate in closest
         * points.
         */
        pts_A[ai++] = *A1;
        pts_A[ai++] = *A3;
        pts_B[bi++] = *B1;
        pts_B[bi++] = *B3;
 
        /*
         * Overlapping circles might have a zero distance
         * case if the circle intersection points are inside both
         * arcs.
         */
        if (is_overlapping)
        {
                /*
                 * Find the two points the circles intersect at.
                 */
                uint32_t npoints = lw_dist2d_circle_circle_intersections(
                        &center_A, radius_A,
                        &center_B, radius_B,
                        intersectionPts);
                for (uint32_t i = 0; i < npoints; i++)
                {
                        /*
                         * If an intersection point is contained in both
                         * arcs, that is a location of zero distance, so
                         * we are done calculating.
                         */
                        if (lw_pt_in_arc(&intersectionPts[i], A1, A2, A3) &&
                                lw_pt_in_arc(&intersectionPts[i], B1, B2, B3))
                        {
                                lw_dist2d_distpts_set(dl, 0.0, &intersectionPts[i], &intersectionPts[i]);
                                return LW_TRUE;
                        }
                }
        }
 
        /*
         * Join the circle centers and find the places that
         * line intersects the circles. Where those places
         * are in the arcs, they are potential sites of the
         * closest points.
         */
        if (is_disjoint || is_contained || is_overlapping)
        {
                if (!is_same_center)
                {
                        /* Add points on A that intersect line from center_A to center_B */
                        lw_dist2d_circle_intersections(
                            A1, A2, A3,
                            &center_A, radius_A, &center_B,
                            pts_A, &ai);
 
                        /* Add points on B that intersect line from center_B to center_A */
                        lw_dist2d_circle_intersections(
                            B1, B2, B3,
                            &center_B, radius_B, &center_A,
                            pts_B, &bi);
                }
 
                /* Add points on A that intersect line to B1 */
                lw_dist2d_circle_intersections(
                    A1, A2, A3,
                    &center_A, radius_A, B1,
                    pts_A, &ai);
 
                /* Add points on A that intersect line to B3 */
                lw_dist2d_circle_intersections(
                    A1, A2, A3,
                    &center_A, radius_A, B3,
                    pts_A, &ai);
 
                /* Add points on B that intersect line to A1 */
                lw_dist2d_circle_intersections(
                    B1, B2, B3,
                    &center_B, radius_B, A1,
                    pts_B, &bi);
 
                /* Add points on B that intersect line to A3 */
                lw_dist2d_circle_intersections(
                    B1, B2, B3,
                    &center_B, radius_B, A3,
                    pts_B, &bi);
        }
 
        /*
         * Now just brute force check all pairs of participating
         * points, to find the pair that is closest together.
         */
        for (uint32_t i = 0; i < ai; i++)
                for (uint32_t j = 0; j < bi; j++)
                        lw_dist2d_pt_pt(&pts_A[i], &pts_B[j], dl);
 
        return LW_TRUE;
}

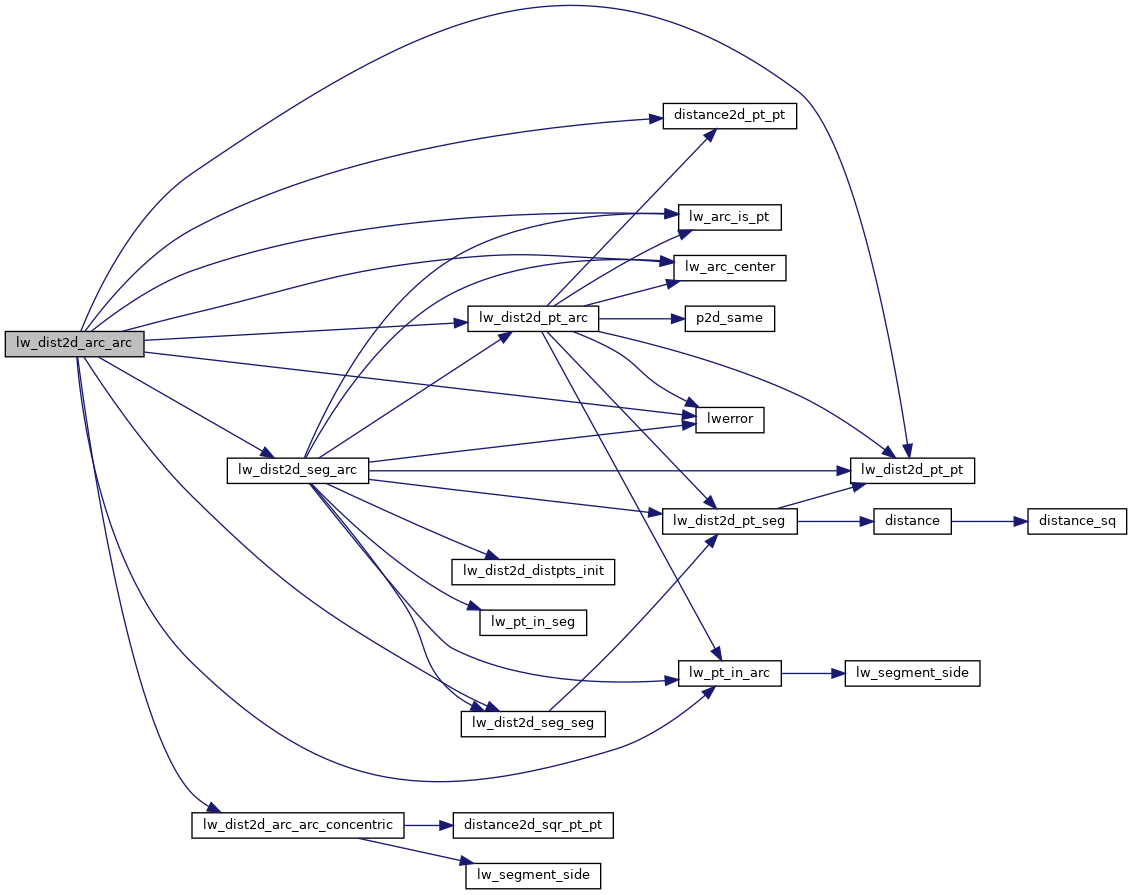
References DIST_MIN, distance2d_pt_pt(), lw_arc_center(), lw_arc_is_pt(), lw_dist2d_circle_circle_intersections(), lw_dist2d_circle_intersections(), lw_dist2d_distpts_set(), lw_dist2d_pt_arc(), lw_dist2d_pt_pt(), lw_dist2d_seg_arc(), lw_dist2d_seg_seg(), lw_pt_in_arc(), LW_TRUE, lwerror(), DISTPTS::mode, and p2d_same().

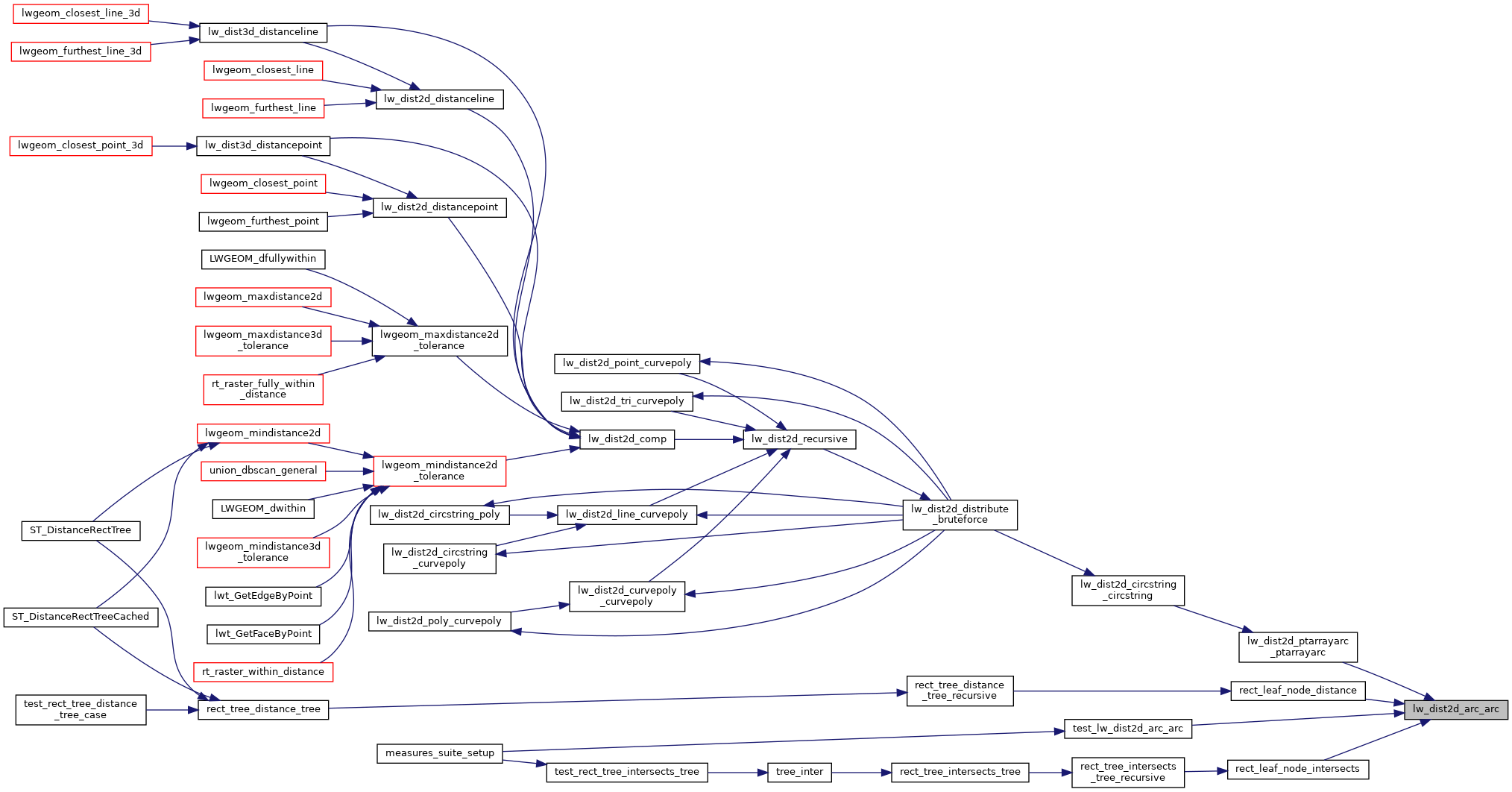
Referenced by lw_dist2d_ptarrayarc_ptarrayarc(), rect_leaf_node_distance(), rect_leaf_node_intersects(), and test_lw_dist2d_arc_arc().

Here is the call graph for this function:

Here is the caller graph for this function: