ptarray_segmentize_sphere()

static POINTARRAY* ptarray_segmentize_sphere ( const POINTARRAY *  pa_in, double  max_seg_length  )

static

Create a new point array with no segment longer than the input segment length (expressed in radians!)

Parameters

pa_in	- input point array pointer
max_seg_length	- maximum output segment length in radians

Definition at line 1638 of file lwgeodetic.c.

{
        POINTARRAY *pa_out;
        int hasz = ptarray_has_z(pa_in);
        int hasm = ptarray_has_m(pa_in);
        POINT4D p1, p2;
        POINT3D q1, q2;
        GEOGRAPHIC_POINT g1, g2;
        uint32_t i;
 
        /* Just crap out on crazy input */
        if ( ! pa_in )
                lwerror("%s: null input pointarray", __func__);
        if ( max_seg_length <= 0.0 )
                lwerror("%s: maximum segment length must be positive", __func__);
 
        /* Empty starting array */
        pa_out = ptarray_construct_empty(hasz, hasm, pa_in->npoints);
 
        /* Simple loop per edge */
        for (i = 1; i < pa_in->npoints; i++)
        {
                getPoint4d_p(pa_in, i-1, &p1);
                getPoint4d_p(pa_in, i, &p2);
                geographic_point_init(p1.x, p1.y, &g1);
                geographic_point_init(p2.x, p2.y, &g2);
 
                /* Skip duplicate points (except in case of 2-point lines!) */
                if ((pa_in->npoints > 2) && p4d_same(&p1, &p2))
                        continue;
 
                /* How long is this edge? */
                double d = sphere_distance(&g1, &g2);
 
                if (d > max_seg_length)
                {
                        geog2cart(&g1, &q1);
                        geog2cart(&g2, &q2);
                        /* 3-d end points, XYZM end point, current edge size, min edge size */
                        ptarray_segmentize_sphere_edge_recursive(&q1, &q2, &p1, &p2, d, max_seg_length, pa_out);
                }
                /* If we don't segmentize, we need to add first point manually */
                else
                {
                        ptarray_append_point(pa_out, &p1, LW_TRUE);
                }
        }
        /* Always add the last point */
        ptarray_append_point(pa_out, &p2, LW_TRUE);
        return pa_out;
}

References geog2cart(), geographic_point_init(), getPoint4d_p(), LW_TRUE, lwerror(), POINTARRAY::npoints, p4d_same(), ptarray_append_point(), ptarray_construct_empty(), ptarray_has_m(), ptarray_has_z(), ptarray_segmentize_sphere_edge_recursive(), sphere_distance(), POINT4D::x, and POINT4D::y.

Referenced by lwgeom_segmentize_sphere().

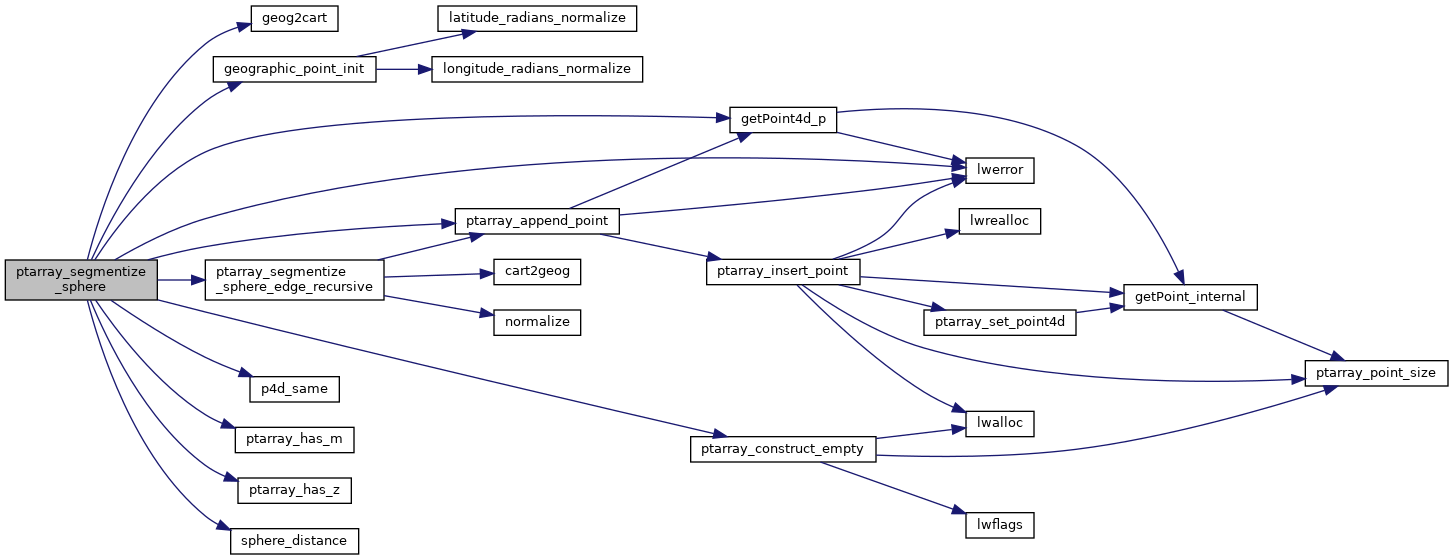
Here is the call graph for this function:

Here is the caller graph for this function: