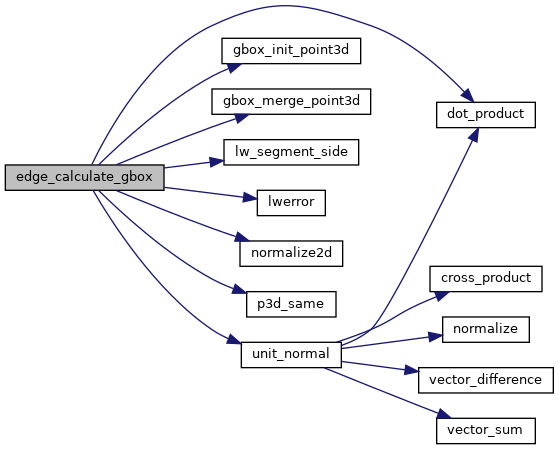
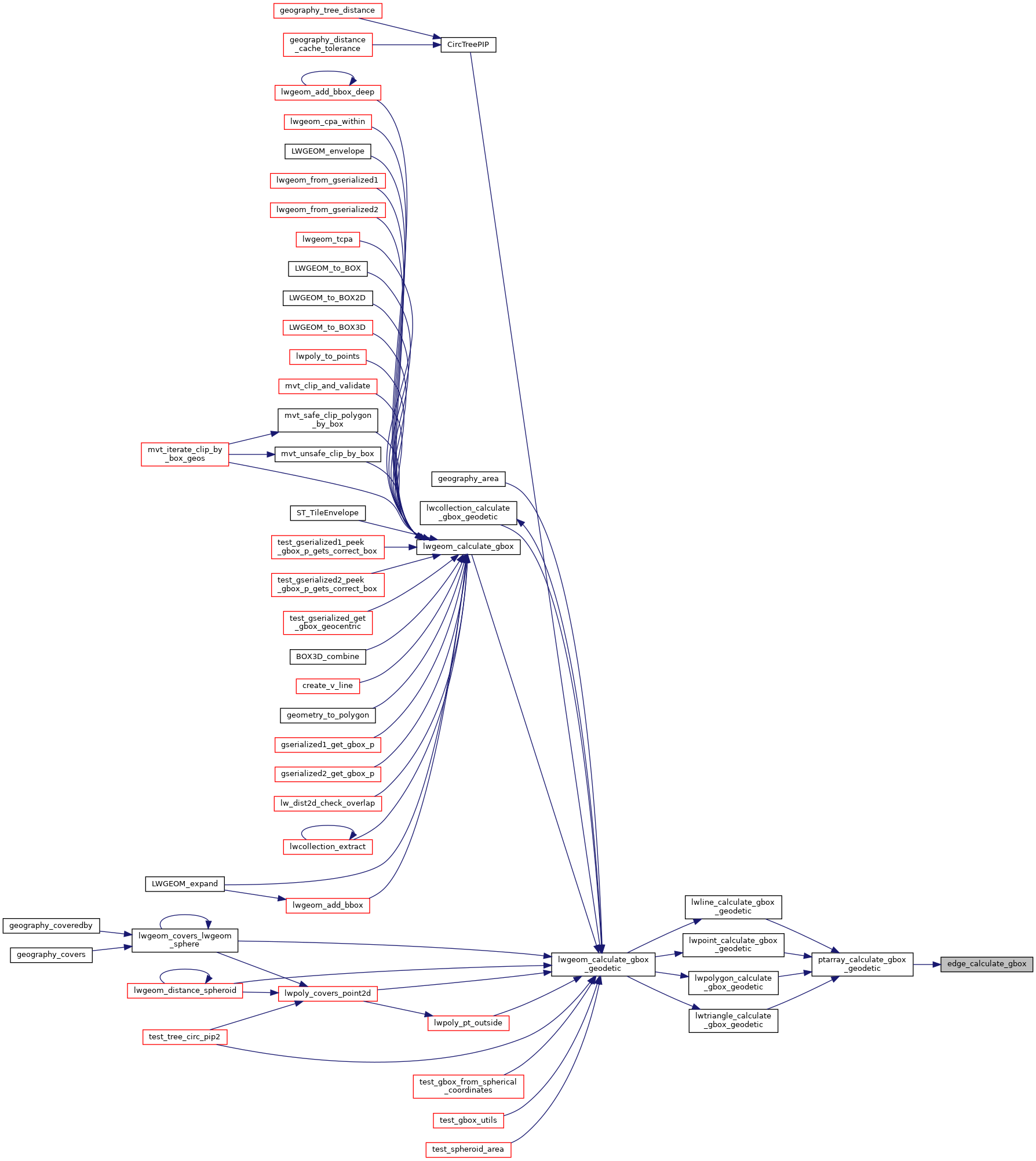
The magic function, given an edge in spherical coordinates, calculate a 3D bounding box that fully contains it, taking into account the curvature of the sphere on which it is inscribed.
Any arc on the sphere defines a plane that bisects the sphere. In this plane, the arc is a portion of a unit circle. Projecting the end points of the axes (1,0,0), (-1,0,0) etc, into the plane and normalizing yields potential extrema points. Those points on the side of the plane-dividing line formed by the end points that is opposite the origin of the plane are extrema and should be added to the bounding box.
Definition at line 1408 of file lwgeodetic.c.
1426 lwerror(
"Antipodal (180 degrees long) edge detected!");
1441 memset(X, 0,
sizeof(
POINT3D) * 6);
1442 X[0].
x = X[2].
y = X[4].
z = 1.0;
1443 X[1].
x = X[3].
y = X[5].
z = -1.0;
1451 for ( i = 0; i < 6; i++ )
1464 Xn.
x = RX.
x * A1->
x + RX.
y * A3.
x;
1465 Xn.
y = RX.
x * A1->
y + RX.
y * A3.
y;
1466 Xn.
z = RX.
x * A1->
z + RX.
y * A3.
z;
int gbox_merge_point3d(const POINT3D *p, GBOX *gbox)
Update the GBOX to be large enough to include itself and the new point.
int gbox_init_point3d(const POINT3D *p, GBOX *gbox)
Initialize a GBOX using the values of the point.
int p3d_same(const POINT3D *p1, const POINT3D *p2)
int lw_segment_side(const POINT2D *p1, const POINT2D *p2, const POINT2D *q)
lw_segment_side()
static void normalize2d(POINT2D *p)
Normalize to a unit vector.
void unit_normal(const POINT3D *P1, const POINT3D *P2, POINT3D *normal)
Calculates the unit normal to two vectors, trying to avoid problems with over-narrow or over-wide cas...
static double dot_product(const POINT3D *p1, const POINT3D *p2)
Convert cartesian coordinates on unit sphere to lon/lat coordinates static void cart2ll(const POINT3D...
void lwerror(const char *fmt,...)
Write a notice out to the error handler.
References dot_product(), FP_EQUALS, gbox_init_point3d(), gbox_merge_point3d(), LW_FAILURE, lw_segment_side(), LW_SUCCESS, lwerror(), normalize2d(), p3d_same(), unit_normal(), POINT2D::x, POINT3D::x, POINT2D::y, POINT3D::y, and POINT3D::z.
Referenced by ptarray_calculate_gbox_geodetic().