24. Рівність

24.1. Рівність

Визначення рівності при роботі з геометрією може бути складним завданням. PostGIS підтримує три різні функції, які можна використовувати для визначення різних рівнів рівності, хоча для більшої зрозумілості ми будемо використовувати наведені нижче визначення. Для ілюстрації цих функцій ми будемо використовувати наступні полігони.

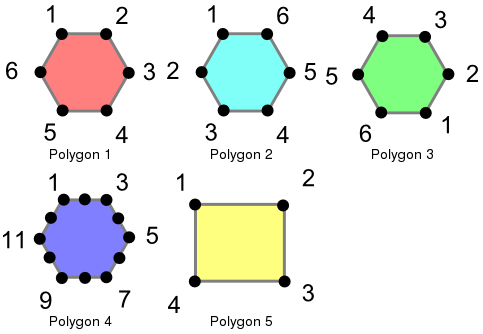
_images/polygon-table.png

Ці багатокутники завантажуються за допомогою наступних команд.

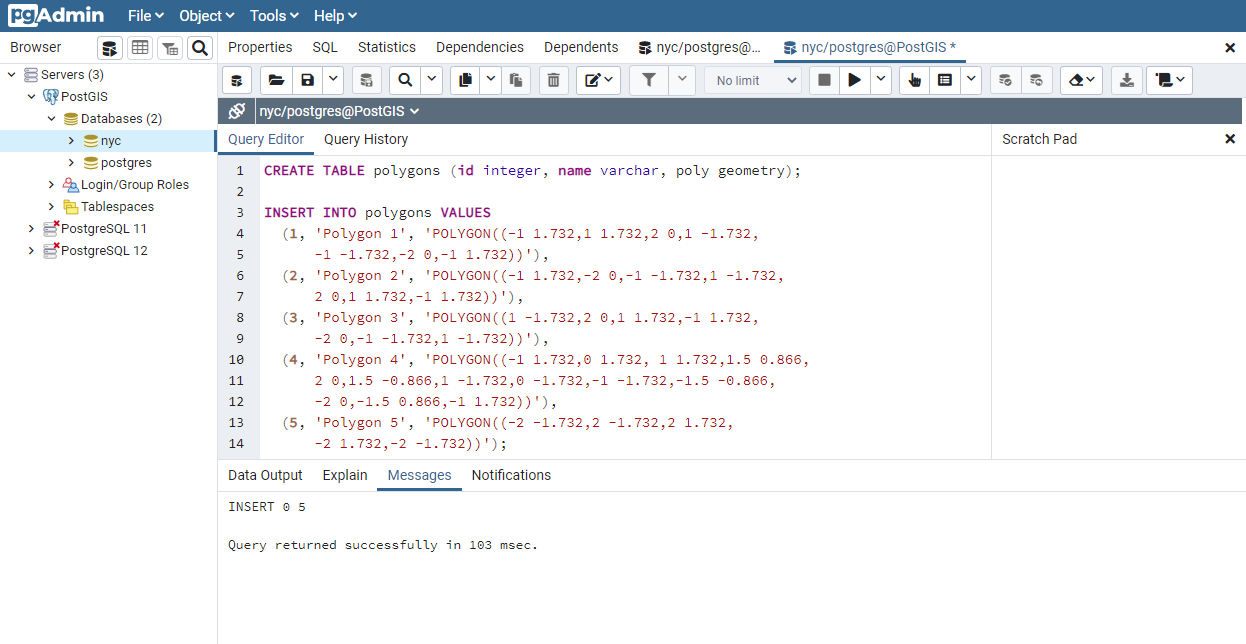
CREATE TABLE polygons (id integer, name varchar, poly geometry);

INSERT INTO polygons VALUES
  (1, 'Polygon 1', 'POLYGON((-1 1.732,1 1.732,2 0,1 -1.732,
      -1 -1.732,-2 0,-1 1.732))'),
  (2, 'Polygon 2', 'POLYGON((-1 1.732,-2 0,-1 -1.732,1 -1.732,
      2 0,1 1.732,-1 1.732))'),
  (3, 'Polygon 3', 'POLYGON((1 -1.732,2 0,1 1.732,-1 1.732,
      -2 0,-1 -1.732,1 -1.732))'),
  (4, 'Polygon 4', 'POLYGON((-1 1.732,0 1.732, 1 1.732,1.5 0.866,
      2 0,1.5 -0.866,1 -1.732,0 -1.732,-1 -1.732,-1.5 -0.866,
      -2 0,-1.5 0.866,-1 1.732))'),
  (5, 'Polygon 5', 'POLYGON((-2 -1.732,2 -1.732,2 1.732,
      -2 1.732,-2 -1.732))');
_images/start13.png

24.1.1. Абсолютно однакові

Абсолютна однаковість визначається шляхом порівняння двох геометрій, вершина за вершиною, послідовно, щоб переконатися, що вони ідентичні за положенням. Наступні приклади показують, як ефективність цього методу може бути обмеженою.

SELECT a.name, b.name,
  CASE WHEN ST_OrderingEquals(a.poly, b.poly)
       THEN 'Exactly Equal'
       ELSE 'Not Exactly Equal' END
  FROM polygons AS a, polygons AS b;
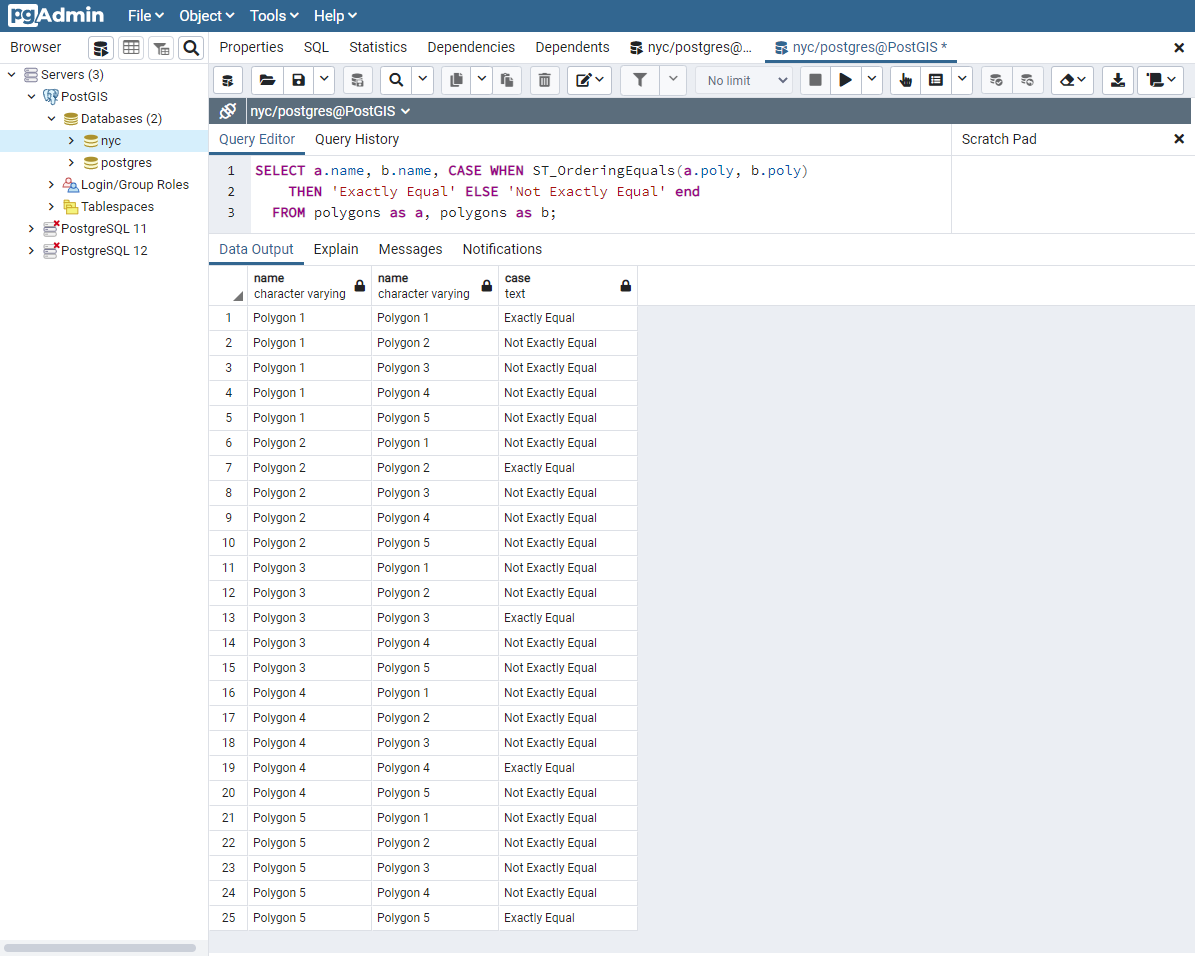
_images/start14.png

У цьому прикладі багатокутники рівні тільки самі собі, а не іншим, на перший погляд, еквівалентним багатокутникам (як у випадку багатокутників 1–3). У випадку багатокутників 1, 2 і 3 вершини знаходяться в однакових положеннях, але визначені в різному порядку. Багатокутник 4 має колінеарні (а отже, надлишкові) вершини на ребрах шестикутника, що спричиняє нерівність з багатокутником 1.

24.1.2. Просторово однакові

Як ми бачили вище, абсолютна однаковість не враховує просторову природу геометрій. Існує функція, яка має відповідну назву ST_Equals, яка дозволяє перевірити просторову однаковість або еквівалентність геометрій.

SELECT a.name, b.name,
  CASE WHEN ST_Equals(a.poly, b.poly)
       THEN 'Spatially Equal'
       ELSE 'Not Equal' END
  FROM polygons AS a, polygons AS b;
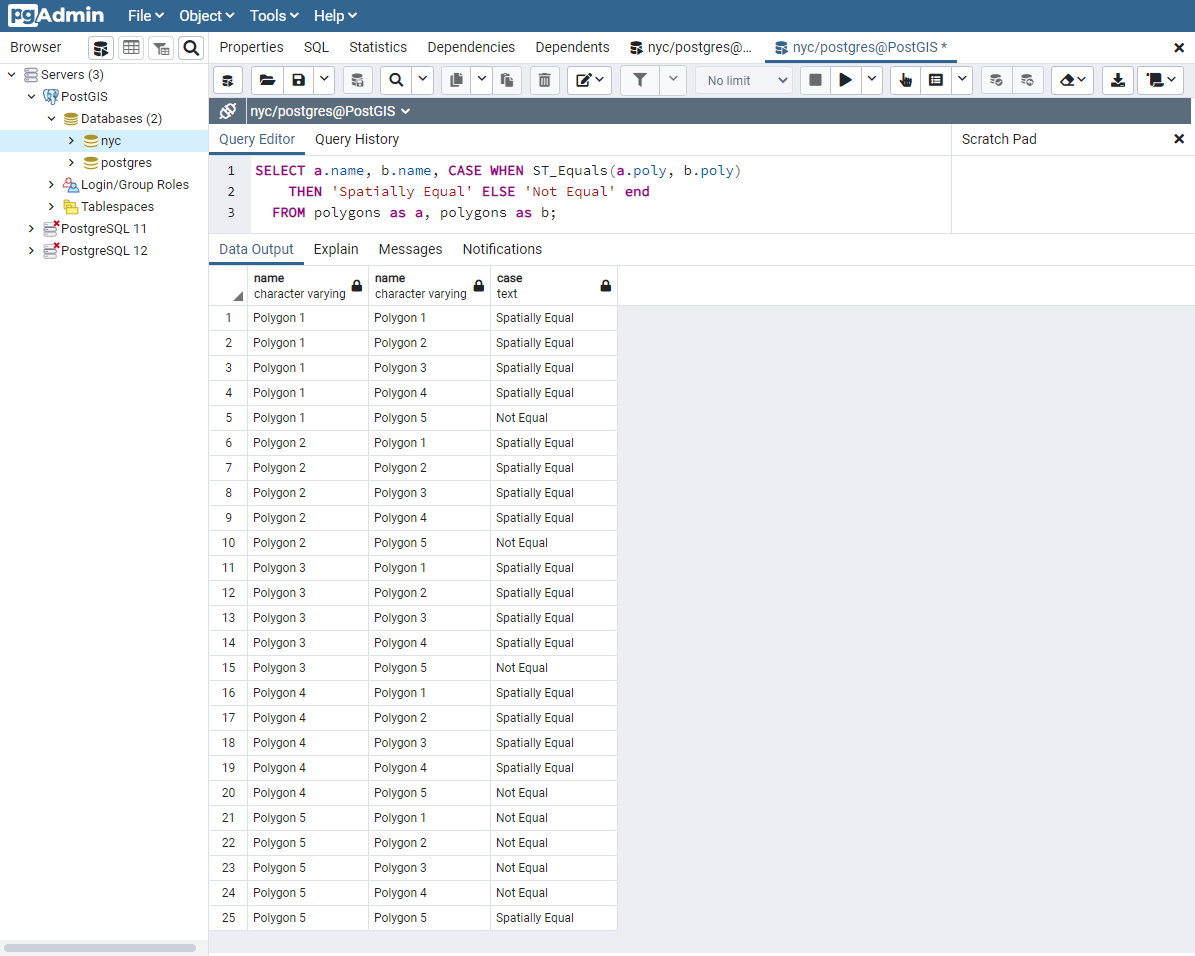
_images/start15.png

Ці результати більше відповідають нашому інтуїтивному розумінню рівності. Полігони від 1 до 4 вважаються однаковими, оскільки вони охоплюють однакову площу. Зверніть увагу, що тут не має значення ні напрямок полігону, ні початкова точка для визначення полігону, ні кількість використаних точок. Важливо те, що полігони містять однаковий простір.

24.1.3. Рівні межі

Абсолютна однаковість вимагає, в найгіршому випадку, порівняння кожної вершини в геометрії для визначення рівності. Це може бути повільним і може бути непридатним для порівняння великої кількості геометрій. Для більш швидкого порівняння передбачений оператор рівних меж ~=. Він працює тільки з обмежувальним прямокутником (прямокутником), гарантуючи, що геометрії займають однакову двовимірну площу, але не обов’язково однаковий простір.

SELECT a.name, b.name,
  CASE WHEN a.poly ~= b.poly
       THEN 'Equal Bounds'
       ELSE 'Non-equal Bounds' END
  FROM polygons AS a, polygons AS b;
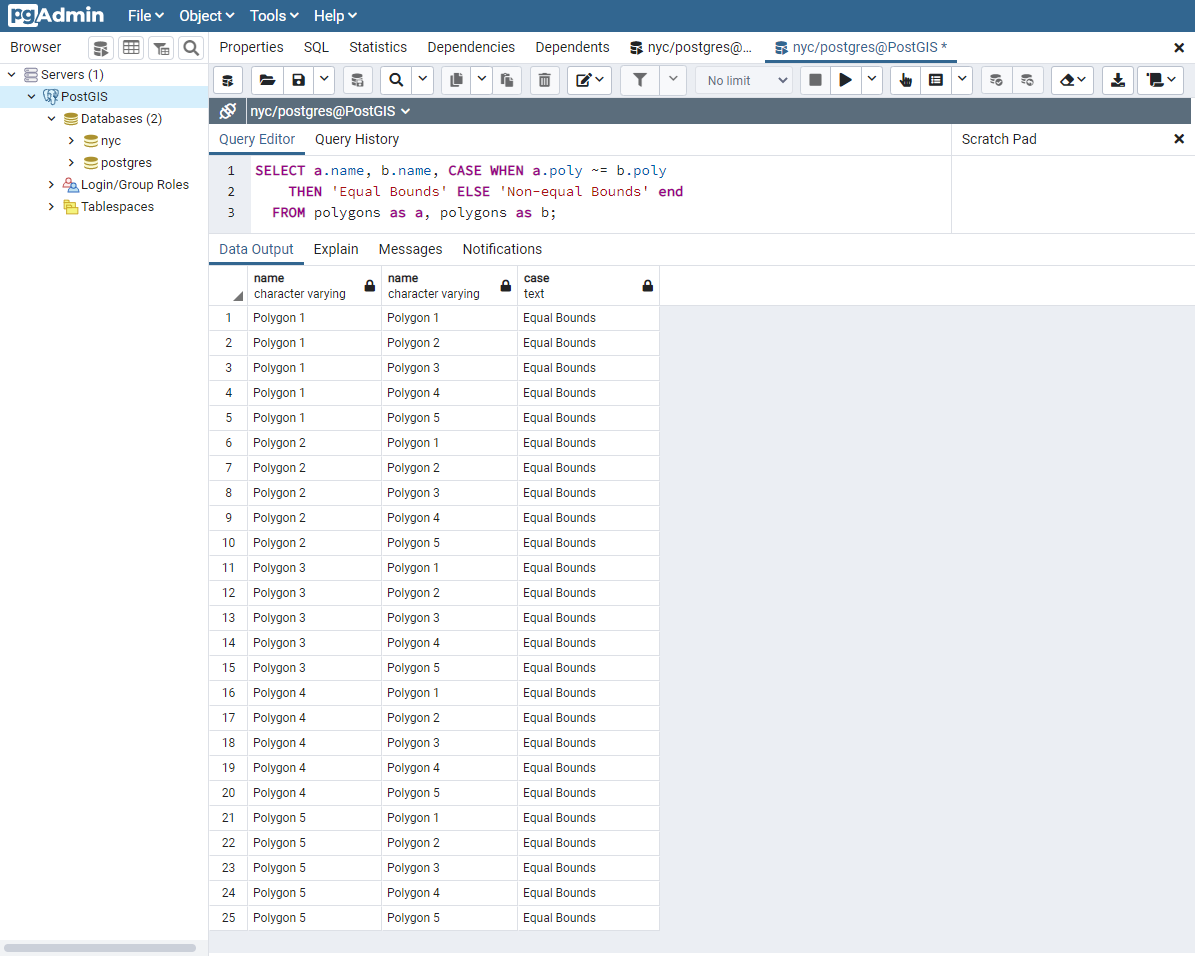
_images/start17.png

Як бачите, всі наші просторово рівні геометрії також мають рівні межі. На жаль, багатокутник 5 також повертається як рівний за результатами цього тесту, оскільки він має ту саму обмежувальну коробку, що й інші геометрії. Чому це корисно? Хоча це буде детально розглянуто пізніше, коротка відповідь полягає в тому, що це дозволяє використовувати просторове індексування, яке може швидко зменшити величезні набори порівнянь до більш керованих блоків під час об’єднання або фільтрування даних.