24. 等価性

24.1. 等価性

ジオメトリを処理する時に同等性の判断が難しいことがあります。PostGIS は、異なる同等性レベルを判定するために使える、三つの異なる機能に対応していますが、分かりやすくするため、下のように定義します。これらの関数を説明するために、次のポリゴンを使用します。

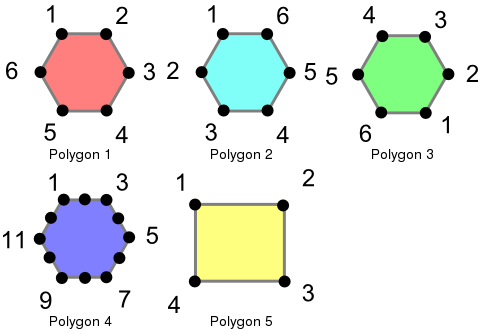
_images/polygon-table.png

これらのポリゴンは次のコマンドを使ってロードされます。

CREATE TABLE polygons (id integer, name varchar, poly geometry);

INSERT INTO polygons VALUES
  (1, 'Polygon 1', 'POLYGON((-1 1.732,1 1.732,2 0,1 -1.732,
      -1 -1.732,-2 0,-1 1.732))'),
  (2, 'Polygon 2', 'POLYGON((-1 1.732,-2 0,-1 -1.732,1 -1.732,
      2 0,1 1.732,-1 1.732))'),
  (3, 'Polygon 3', 'POLYGON((1 -1.732,2 0,1 1.732,-1 1.732,
      -2 0,-1 -1.732,1 -1.732))'),
  (4, 'Polygon 4', 'POLYGON((-1 1.732,0 1.732, 1 1.732,1.5 0.866,
      2 0,1.5 -0.866,1 -1.732,0 -1.732,-1 -1.732,-1.5 -0.866,
      -2 0,-1.5 0.866,-1 1.732))'),
  (5, 'Polygon 5', 'POLYGON((-2 -1.732,2 -1.732,2 1.732,
      -2 1.732,-2 -1.732))');
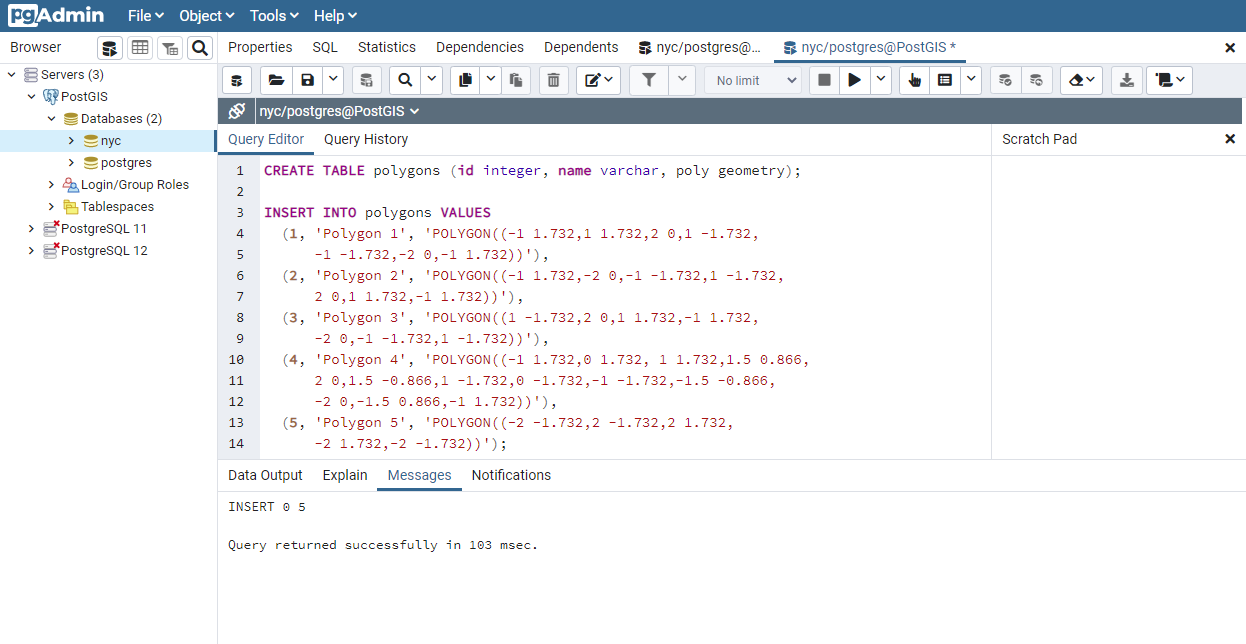
_images/start13.png

24.1.1. 確実に等価

確実な等価性は二つのジオメトリの頂点と頂点を順序も含めて、同一の位置にあるかを比較して決めます。次の例ではこのメソッドでの有効性がどれだけ制限されるかを示しています。

SELECT a.name, b.name,
  CASE WHEN ST_OrderingEquals(a.poly, b.poly)
       THEN 'Exactly Equal'
       ELSE 'Not Exactly Equal' END
  FROM polygons AS a, polygons AS b;
_images/start14.png

この例では、ポリゴンは自身としか等しくなく、他の等価に見えるポリゴンとは等しくありません (ポリゴン1から3の場合)。ポリゴン 1, 2, 3 の場合は、頂点は同じ位置にありますが、順序が異なります。ポリゴン 4 は、六角形の辺の上で共線が存在する (ゆえに冗長です) ので、ポリゴン 1 と等価でなくなります。

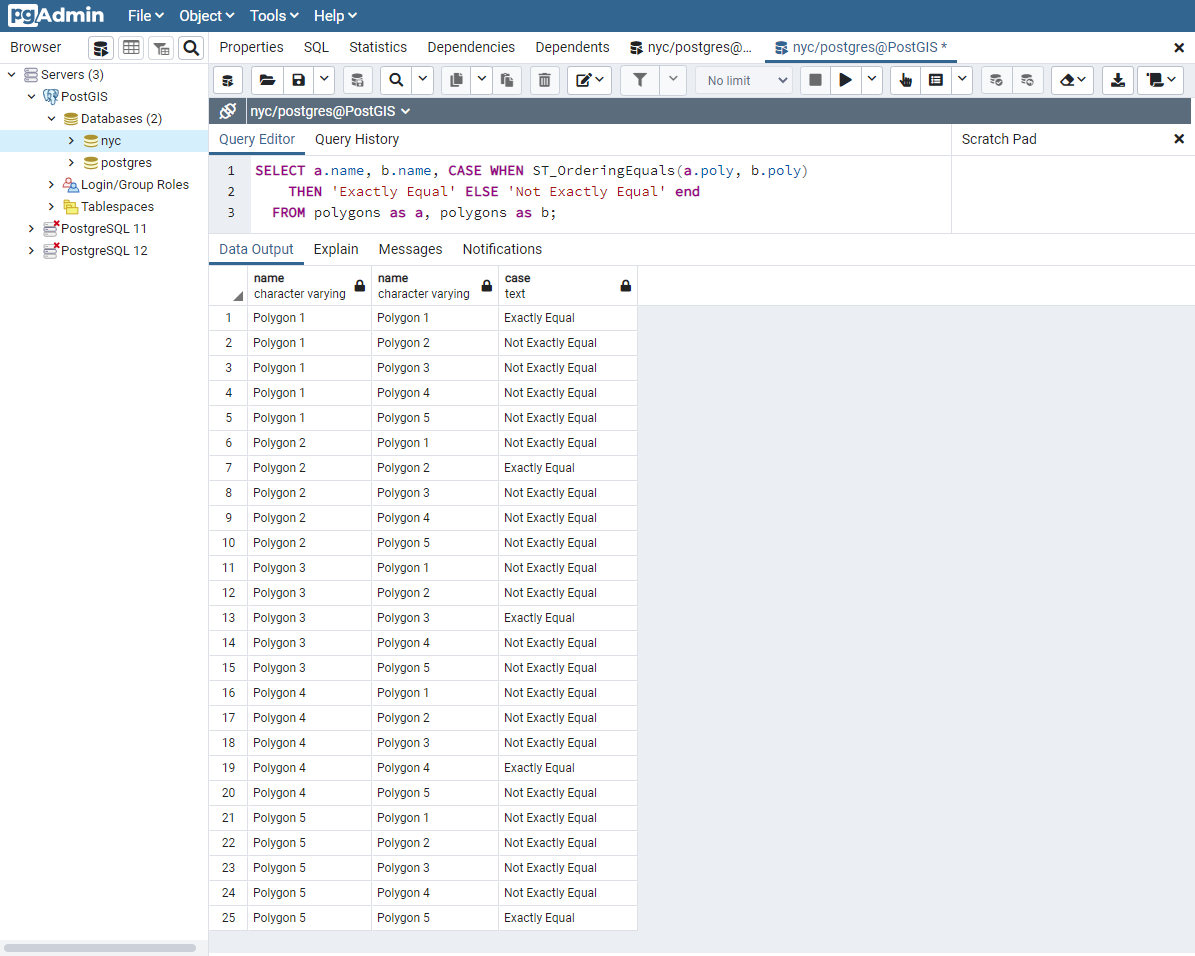
24.1.2. 空間的に等価

上に見る通り、確実な等価性は、ジオメトリの空間の性質を考慮に入れていません。適切に名付けられた ST_Equals 関数があり、空間的な等価性のテスト、もしくは、ジオメトリの等価性のテストができます。

SELECT a.name, b.name,
  CASE WHEN ST_Equals(a.poly, b.poly)
       THEN 'Spatially Equal'
       ELSE 'Not Equal' END
  FROM polygons AS a, polygons AS b;
_images/start15.png

これらの結果は、等価性の直感的な理解との一致がよりよくなります。ポリゴン 1 から 4 は、同じ領域を囲んでいるので、等価とみなされます。ポリゴンの方向、ポリゴンの定義のための開始点、ポイント数のいずれもが、ここでは重要ではないことに注意して下さい。重要なのは、ポリゴンが同じ空間を含むことなのです。

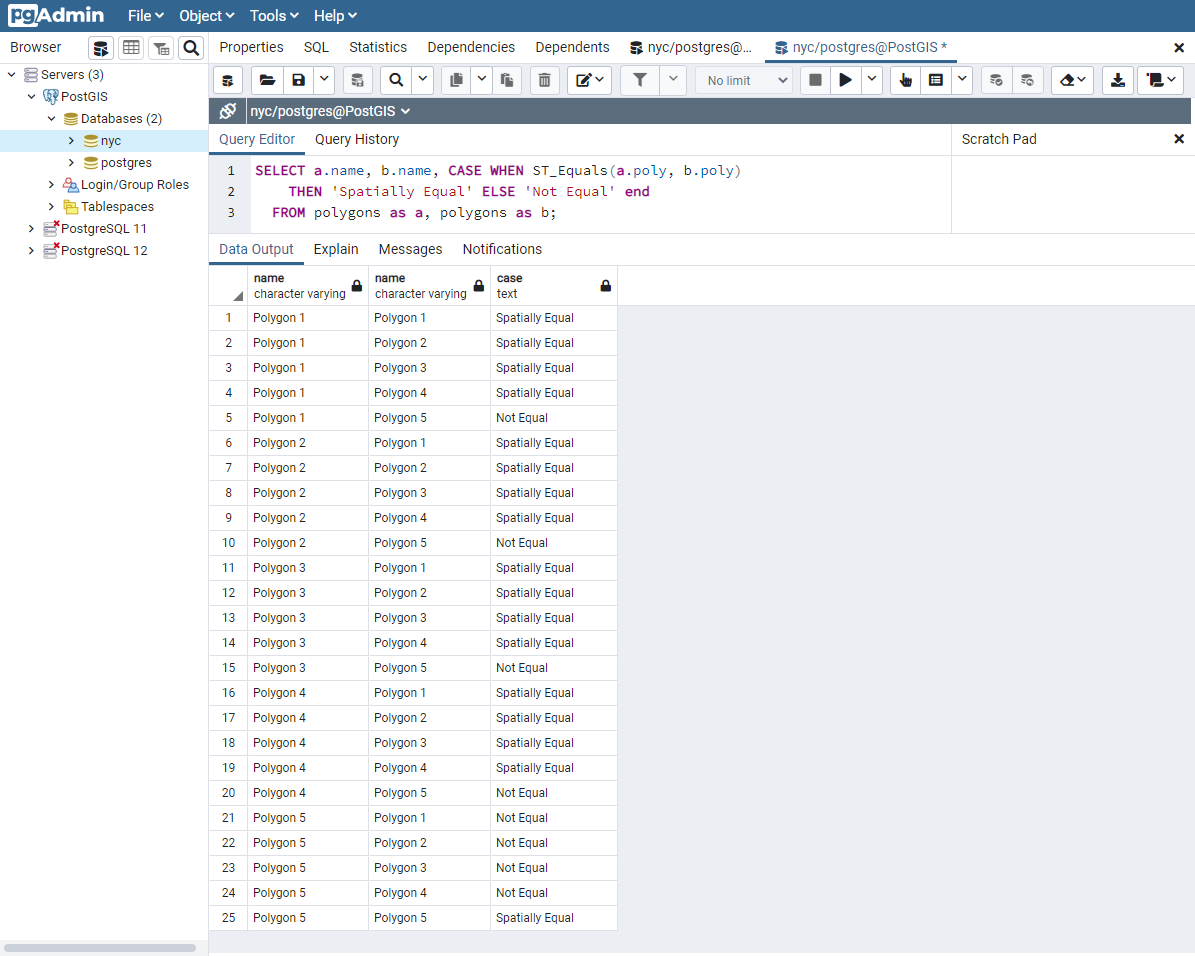
24.1.3. 境界が等価

確実な等価性には、最悪の場合には、等価性を判断するためにジオメトリの各々の頂点の比較が求められます。これは非常に遅くなりますし、多数のジオメトリの比較には適切でない場合があります。より高速な比較のために、バウンディングボックスの等価性を見る演算子である ~= が提供されています。この演算子はバウンディングボックス (長方形) だけで計算していて、ジオメトリが同じ二次元範囲を占めるのを保証しますが、同じ空間を占めている保証はしません。

SELECT a.name, b.name,
  CASE WHEN a.poly ~= b.poly
       THEN 'Equal Bounds'
       ELSE 'Non-equal Bounds' END
  FROM polygons AS a, polygons AS b;
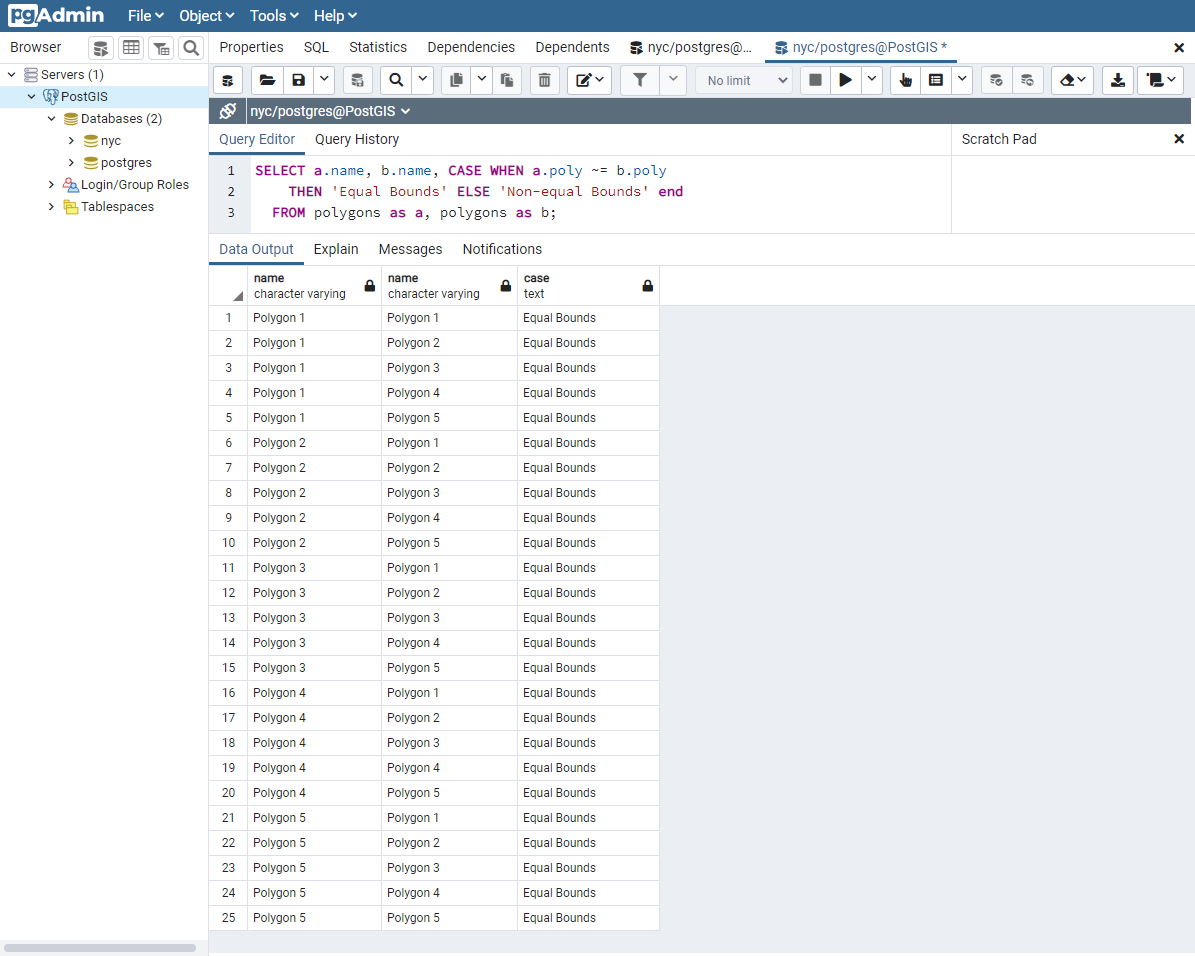
_images/start17.png

ご覧の通り、全ての空間的に等価はバウンディングボックスも等価です。不幸なことに、ポリゴン 5 はこのテストしたで等価とされます。他のジオメトリと同じバウンディングボックスとなるためです。ではなぜこれが便利なのでしょうか？後で詳細説明をしますが、簡単に言うと、この方法だと、空間インデックスを使えて、データの結合やフィルタリングの時に、巨大な比較対象の集合を、より管理しやすいブロックに素早く減らすことができるためです。