24. Igualdad

24.1. Igualdad

Determinar la igualdad cuando se trata de geometrías puede ser complicado. PostGIS soporta tres funciones diferentes que se pueden utilizar para determinar los diferentes niveles de igualdad, aunque para mayor claridad vamos a utilizar las definiciones a continuación. Para ilustrar estas funciones, utilizaremos los siguientes polígonos.

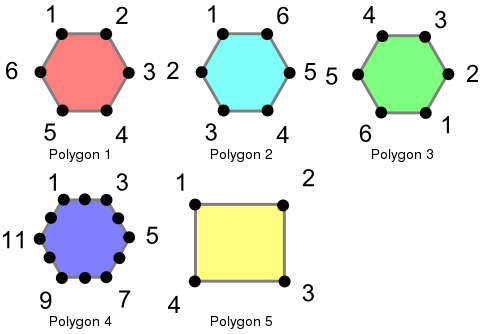
Estos polígonos se cargan utilizando los siguientes comandos.

CREATE TABLE polygons (id integer, name varchar, poly geometry);

INSERT INTO polygons VALUES
  (1, 'Polygon 1', 'POLYGON((-1 1.732,1 1.732,2 0,1 -1.732,
      -1 -1.732,-2 0,-1 1.732))'),
  (2, 'Polygon 2', 'POLYGON((-1 1.732,-2 0,-1 -1.732,1 -1.732,
      2 0,1 1.732,-1 1.732))'),
  (3, 'Polygon 3', 'POLYGON((1 -1.732,2 0,1 1.732,-1 1.732,
      -2 0,-1 -1.732,1 -1.732))'),
  (4, 'Polygon 4', 'POLYGON((-1 1.732,0 1.732, 1 1.732,1.5 0.866,
      2 0,1.5 -0.866,1 -1.732,0 -1.732,-1 -1.732,-1.5 -0.866,
      -2 0,-1.5 0.866,-1 1.732))'),
  (5, 'Polygon 5', 'POLYGON((-2 -1.732,2 -1.732,2 1.732,
      -2 1.732,-2 -1.732))');

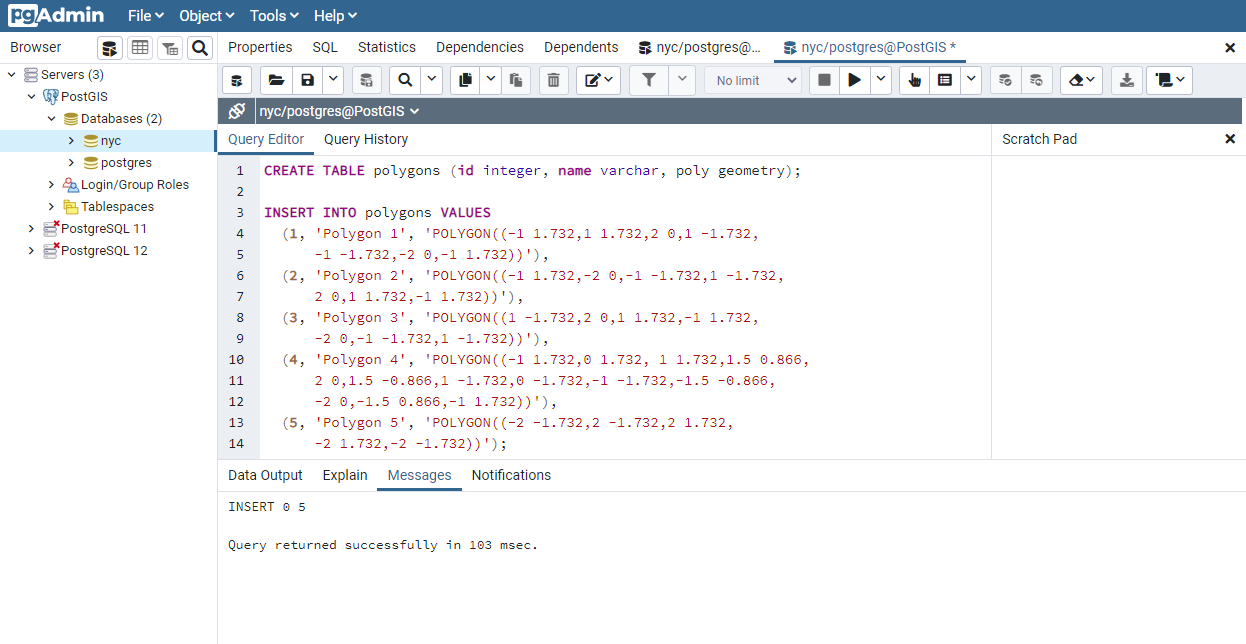
24.1.1. Exactamente igual

La igualdad exacta se determina comparando dos geometrías, vértice por vértice, en orden, para asegurarse de que son idénticas en posición. Los siguientes ejemplos muestran cómo este método puede tener una eficacia limitada.

SELECT a.name, b.name,
  CASE WHEN ST_OrderingEquals(a.poly, b.poly)
       THEN 'Exactly Equal'
       ELSE 'Not Exactly Equal' END
  FROM polygons AS a, polygons AS b;

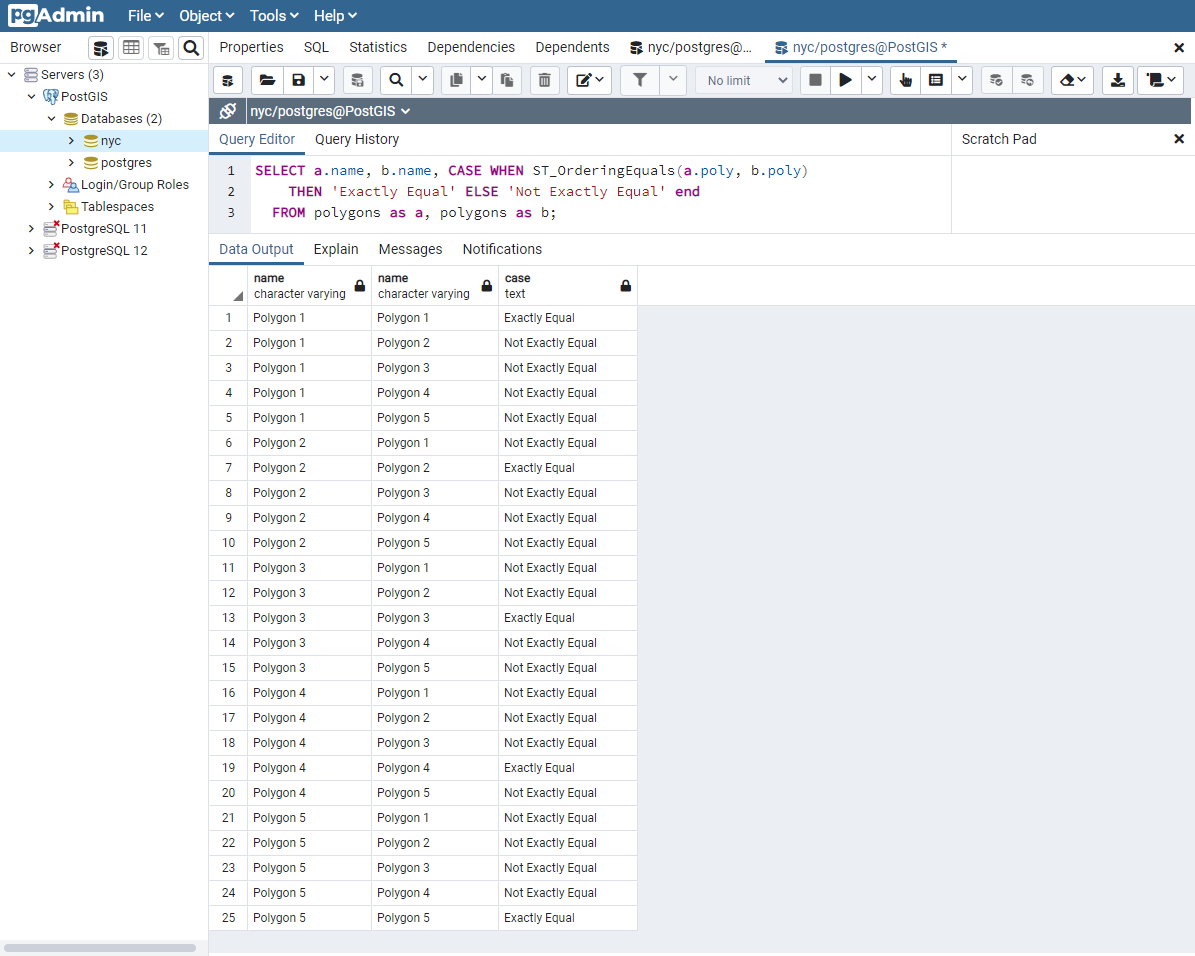
En este ejemplo, los polígonos sólo son iguales a sí mismos, no a otros polígonos aparentemente equivalentes (como en el caso de los polígonos 1 a 3). En el caso de los polígonos 1, 2 y 3, los vértices se encuentran en posiciones idénticas, pero están definidos en órdenes diferentes. El polígono 4 tiene vértices colineales (y, por tanto, redundantes) en los bordes del hexágono, lo que provoca una desigualdad con el polígono 1.

24.1.2. Espacialmente igual

Como hemos visto anteriormente, la igualdad exacta no tiene en cuenta la naturaleza espacial de las geometrías. Existe una función, acertadamente denominada ST_Equals, disponible para comprobar la igualdad o equivalencia espacial de las geometrías.

SELECT a.name, b.name,
  CASE WHEN ST_Equals(a.poly, b.poly)
       THEN 'Spatially Equal'
       ELSE 'Not Equal' END
  FROM polygons AS a, polygons AS b;

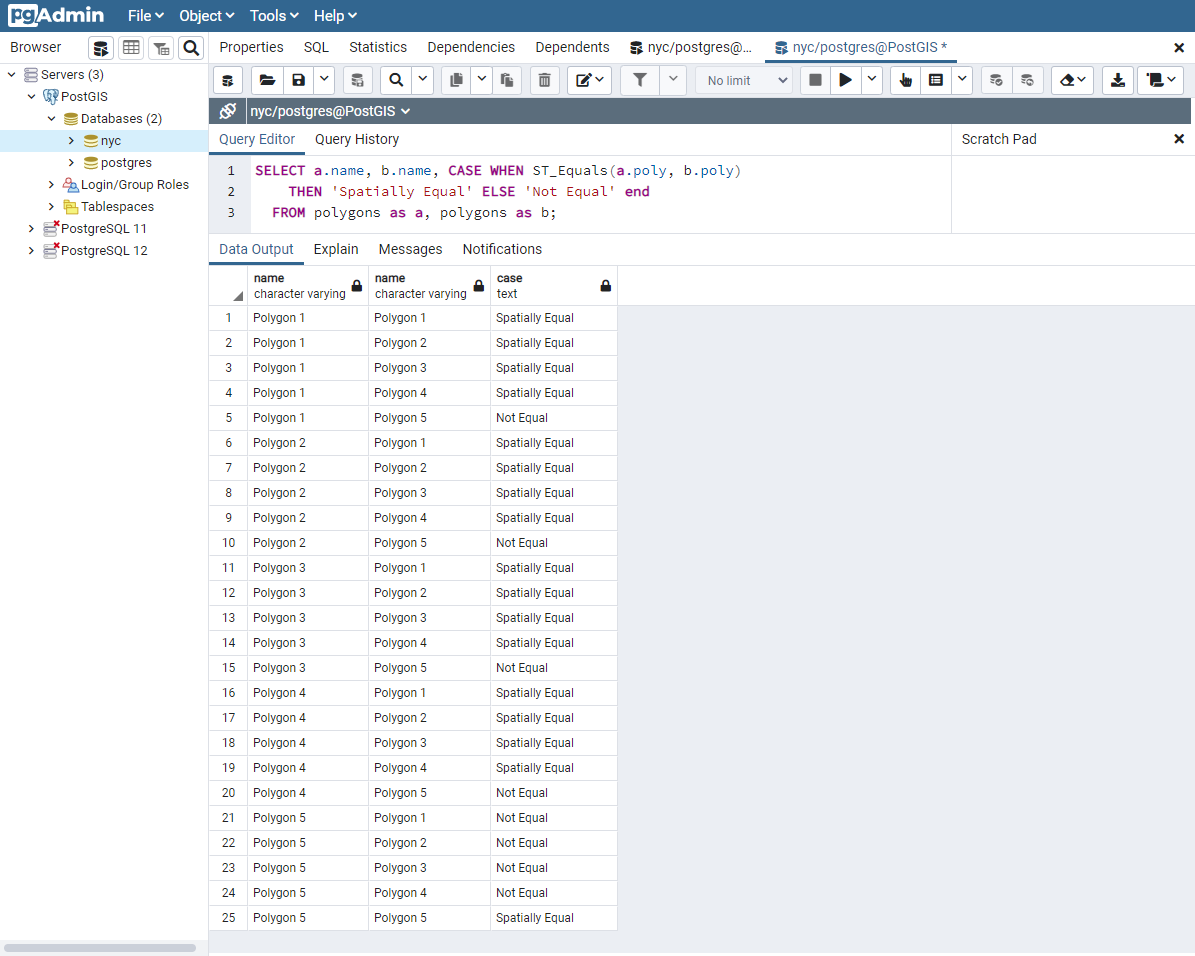
Estos resultados son más acordes con nuestra comprensión intuitiva de la igualdad. Los polígonos 1 a 4 se consideran iguales, ya que encierran la misma área. Observe que ni la dirección en la que se dibuja el polígono, ni el punto de partida para definir el polígono, ni el número de puntos utilizados son importantes aquí. Lo importante es que los polígonos contengan el mismo espacio.

24.1.3. Límites iguales

La igualdad exacta requiere, en el peor de los casos, la comparación de todos y cada uno de los vértices de la geometría para determinar la igualdad. Esto puede ser lento, y puede no ser apropiado para comparar un gran número de geometrías. Para permitir una comparación más rápida, se proporciona el operador de límites iguales, :comando:`~=`. Este operador sólo opera en el rectángulo, garantizando que las geometrías ocupan la misma extensión bidimensional, pero no necesariamente el mismo espacio.

SELECT a.name, b.name,
  CASE WHEN a.poly ~= b.poly
       THEN 'Equal Bounds'
       ELSE 'Non-equal Bounds' END
  FROM polygons AS a, polygons AS b;

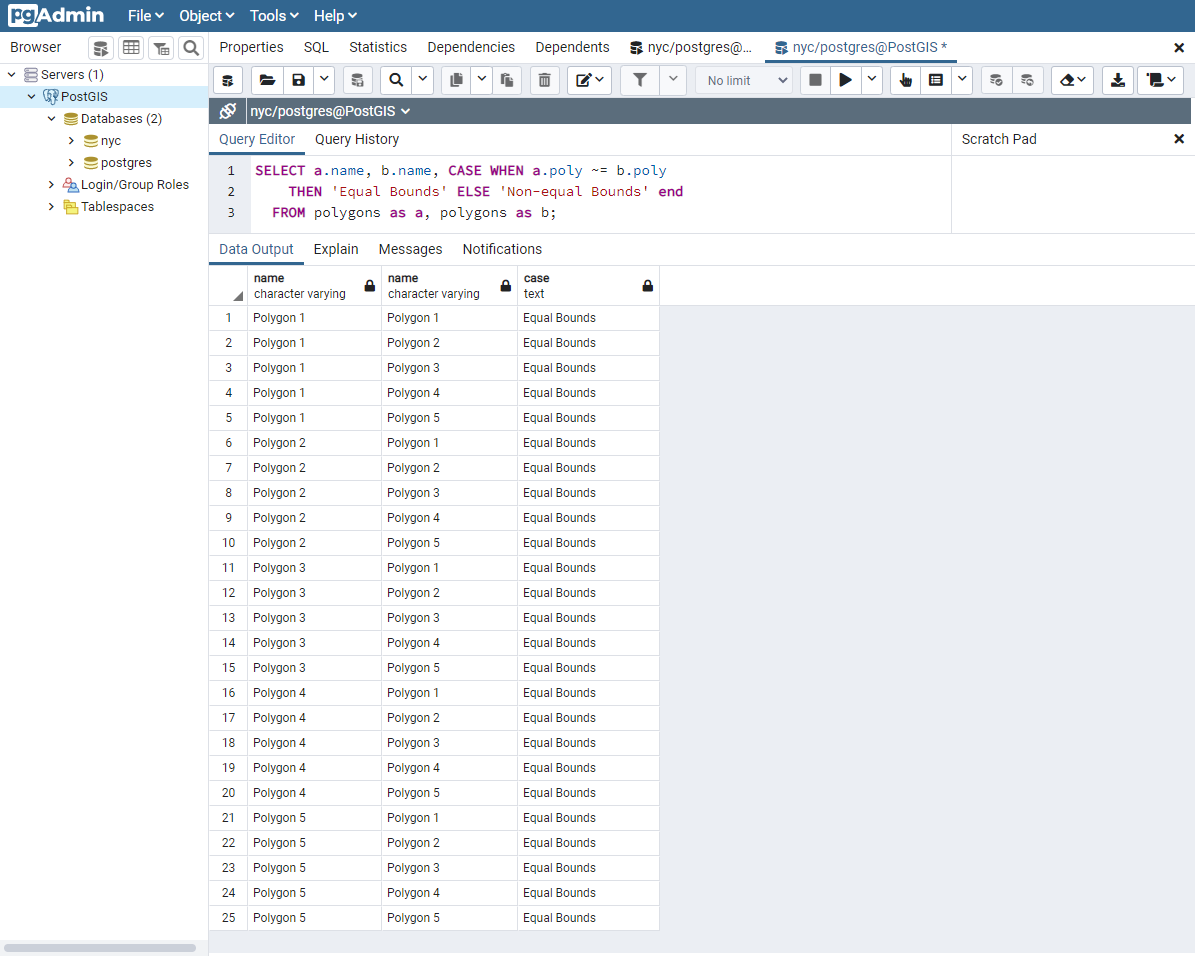
Como puede ver, todas nuestras geometrías espacialmente iguales también tienen límites iguales. Desafortunadamente, el Polígono 5 también se devuelve como igual bajo esta prueba, porque comparte la misma caja delimitadora que las otras geometrías. ¿Por qué es útil? Aunque esto se tratará en detalle más adelante, la respuesta corta es que esto permite el uso de indexación espacial que puede reducir rápidamente enormes conjuntos de comparación en bloques más manejables al unir o filtrar datos.