説明

ジオメトリAがジオメトリBを含む場合にはTRUEを返します。AがBを含むというのは、Bのポイントの全てがAの内側 (つまりAの内部または境界)にあり (Aの外部にBのポイントが全くないとも言えます)、かつBの内部の少なくとも一つのポイントがAの内部にある場合に限ります。

数学用語では: ST_Contains(A, B) ⇔ (A ⋂ B = B) ∧ (Int(A) ⋂ Int(B) ≠ ∅)

包含関係は反射関係です。あらゆるジオメトリは自己を包含します (対照的にST_ContainsProperly述語内ではジオメトリは確実な包含にはなりません)。また、包含関係は非対称です。ST_Contains(A,B) = trueかつST_Contains(B,A) = trueの場合には、二つのジオメトリはトポロジ的に等価です (ST_Equals(A,B) = true)。

ST_ContainsはST_Withinの反対です。ST_Contains(A,B) = ST_Within(B,A)となります。

GEOSモジュールで実現しています。

Enhanced: 2.3.0 PIP short-circuit (ポリゴンとポイントに限定した高速判定)を少ないポイントからなるマルチポイントに対応することができるよう拡張しました。以前の版ではポリゴンとポイントの組み合わせにだけ対応していました。

ご注意: これは論理値を返して整数を返さないのが「許される」版です。

このメソッドはOGC Simple Features Implementation Specification for SQL 1.1の実装です。 s2.1.1.2 // s2.1.13.3 - within(geometry B, geometry A)と同じ

このメソッドはSQL/MM仕様の実装です。 SQL-MM 3: 5.1.31

例

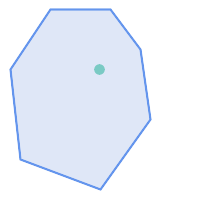
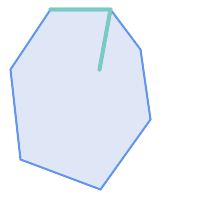
次に示す図全てで、ST_ContainsはTRUEを返します。

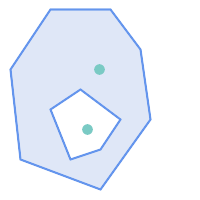
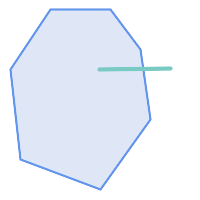
次に示す状況ではST_ContainsはFALSEを返します。

次に示す状況にあっては、内部のインタセクトの状態のために (ST_CoversだとTRUEを返すのに)ST_ContainsはFALSEを返します。

-- A circle within a circle
SELECT ST_Contains(smallc, bigc) As smallcontainsbig,
     ST_Contains(bigc,smallc) As bigcontainssmall,
     ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,
     ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
     ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
     ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
       ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;

-- Result
  smallcontainsbig | bigcontainssmall | bigcontainsunion | bigisunion | bigcoversexterior | bigcontainsexterior
------------------+------------------+------------------+------------+-------------------+---------------------
 f                | t                | t                | t          | t        | f

-- Example demonstrating difference between contains and contains properly
SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, ST_ContainsProperly(geomA, geomA) AS acontainspropa,
   ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),
       ( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),
       ( ST_Point(1,1) )
    ) As foo(geomA);

  geomtype    | acontainsa | acontainspropa | acontainsba | acontainspropba
--------------+------------+----------------+-------------+-----------------
ST_Polygon    | t          | f              | f           | f
ST_LineString | t          | f              | f           | f
ST_Point      | t          | t              | f           | f

 

関連情報

ST_Boundary, ST_ContainsProperly, ST_Covers, ST_CoveredBy, ST_Equals, ST_Within