Name
ST_Contains — Tests if every point of B lies in A, and their interiors have a point in common
Synopsis
boolean ST_Contains(geometry
geomA, geometry
geomB);
Description
Returns TRUE if geometry A contains geometry B. A contains B if and only if all points of B lie inside (i.e. in the interior or boundary of) A (or equivalently, no points of B lie in the exterior of A), and the interiors of A and B have at least one point in common.
In mathematical terms: ST_Contains(A, B) ⇔ (A ⋂ B = B) ∧ (Int(A) ⋂ Int(B) ≠ ∅)
The contains relationship is reflexive: every geometry contains itself.
(In contrast, in the ST_ContainsProperly
predicate a geometry does not properly contain itself.)
The relationship is antisymmetric: if ST_Contains(A,B) = true and ST_Contains(B,A) = true, then
the two geometries must be topologically equal (ST_Equals(A,B) = true).
ST_Contains is the converse of ST_Within.
So, ST_Contains(A,B) = ST_Within(B,A).
![[Note]](../images/note.png)
|
|
|
Because the interiors must have a common point, a subtlety of the definition is that polygons and lines do not contain lines and points lying fully in their boundary. For further details see Subtleties of OGC Covers, Contains, Within. The ST_Covers predicate provides a more inclusive relationship. |
![[Note]](../images/note.png)
|
|
|
This function automatically includes a bounding box comparison
that makes use of any spatial indexes that are available on the geometries.
To avoid index use, use the function |
Performed by the GEOS module
Enhanced: 2.3.0 Enhancement to PIP short-circuit extended to support MultiPoints with few points. Prior versions only supported point in polygon.
![[Important]](../images/important.png)
|
|
|
Enhanced: 3.0.0 enabled support for |
![[Important]](../images/important.png)
|
|
|
Do not use this function with invalid geometries. You will get unexpected results. |
NOTE: this is the "allowable" version that returns a boolean, not an integer.
 This method implements the OGC Simple Features
Implementation Specification for SQL 1.1.
s2.1.1.2 // s2.1.13.3
- same as within(geometry B, geometry A)
This method implements the OGC Simple Features
Implementation Specification for SQL 1.1.
s2.1.1.2 // s2.1.13.3
- same as within(geometry B, geometry A)
 This method implements the SQL/MM specification.
SQL-MM 3: 5.1.31
This method implements the SQL/MM specification.
SQL-MM 3: 5.1.31
Examples
ST_Contains returns TRUE in the following situations:

|
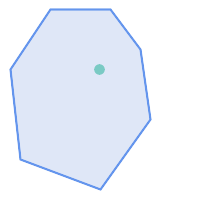
|
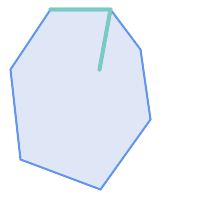
|

|
ST_Contains returns FALSE in the following situations:
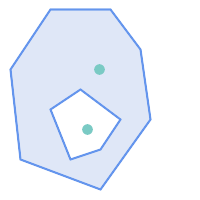
|
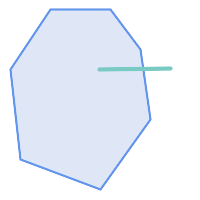
|
Due to the interior intersection condition ST_Contains returns FALSE in the following situations
(whereas ST_Covers returns TRUE):

|
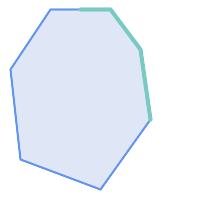
|
-- A circle within a circle
SELECT ST_Contains(smallc, bigc) As smallcontainsbig,
ST_Contains(bigc,smallc) As bigcontainssmall,
ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,
ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;
-- Result
smallcontainsbig | bigcontainssmall | bigcontainsunion | bigisunion | bigcoversexterior | bigcontainsexterior
------------------+------------------+------------------+------------+-------------------+---------------------
f | t | t | t | t | f
-- Example demonstrating difference between contains and contains properly
SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, ST_ContainsProperly(geomA, geomA) AS acontainspropa,
ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),
( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),
( ST_Point(1,1) )
) As foo(geomA);
geomtype | acontainsa | acontainspropa | acontainsba | acontainspropba
--------------+------------+----------------+-------------+-----------------
ST_Polygon | t | f | f | f
ST_LineString | t | f | f | f
ST_Point | t | t | f | f
See Also
ST_Boundary, ST_ContainsProperly, ST_Covers, ST_CoveredBy, ST_Equals, ST_Within