Name
ST_LargestEmptyCircle — Berechnet den größten Kreis, der eine Geometrie nicht überschneidet.
Synopsis
(geometry, geometry, double precision) ST_LargestEmptyCircle(geometry geom, double precision tolerance=0.0, geometry boundary=POINT EMPTY);
Beschreibung
Findet den größten Kreis, der einen Satz von Punkt- und Linienhindernissen nicht überschneidet. (Polygonale Geometrien können als Hindernisse einbezogen werden, aber nur ihre Begrenzungslinien werden verwendet). Der Mittelpunkt des Kreises muss innerhalb einer polygonalen Begrenzung liegen, die standardmäßig die konvexe Hülle der Eingabegeometrie ist. Der Kreismittelpunkt ist der Punkt im Inneren der Begrenzung, der den weitesten Abstand zu den Hindernissen hat. Der Kreis selbst wird durch den Mittelpunkt und einen nächstgelegenen Punkt auf einem Hindernis gebildet, der den Radius des Kreises bestimmt.
Der Kreismittelpunkt wird mit einem iterativen Algorithmus mit einer bestimmten Genauigkeit bestimmt, die durch eine Abstandstoleranz festgelegt wird. Wenn der Genauigkeitsabstand nicht angegeben ist, wird ein angemessener Standardwert verwendet.
Gibt einen Datensatz mit Feldern zurück:
-
center- Mittelpunkt des Kreises -
nächstgelegener- ein Punkt auf der Geometrie, der dem Zentrum am nächsten liegt -
Radius- Radius des Kreises
Um den größten leeren Kreis im Inneren eines Polygons zu finden, siehe ST_MaximumInscribedCircle.
Verfügbarkeit: 3.4.0.
Erfordert GEOS >= 3.9.0.
Beispiele
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
'MULTILINESTRING (
(10 100, 60 180, 130 150, 190 160),
(20 50, 70 70, 90 20, 110 40),
(160 30, 100 100, 180 100))');
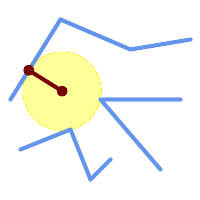
Größter leerer Kreis innerhalb einer Reihe von Linien.
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
ST_Collect(
'MULTIPOINT ((70 50), (60 130), (130 150), (80 90))'::geometry,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry),
0,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry
);
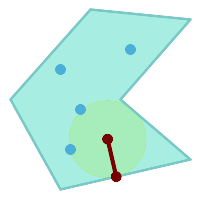
Größter leerer Kreis innerhalb einer Gruppe von Punkten, der in einem Polygon liegen muss. Die Begrenzung des Polygons muss sowohl als Hindernis als auch als Beschränkung für den Kreismittelpunkt angegeben werden.