Name
ST_DelaunayTriangles — Gibt die Delaunay-Triangulation der Scheitelpunkte einer Geometrie zurück.
Synopsis
geometry ST_DelaunayTriangles(geometry g1, float tolerance = 0.0, int4 flags = 0);
Beschreibung
Berechnet die Delaunay-Triangulation der Scheitelpunkte der Eingabegeometrie. Die optionale Toleranz kann verwendet werden, um nahegelegene Eingabepunkte zusammenzufassen, was in einigen Situationen die Robustheit verbessert. Die Ergebnisgeometrie wird durch die konvexe Hülle der Eingabescheitelpunkte begrenzt. Die Darstellung der Ergebnisgeometrie wird durch den Code flags bestimmt:
-
0- eine GEOMETRIESAMMLUNG von dreieckigen POLYGONEN (Standard) -
1- ein MULTILINESTRING der Kanten der Triangulation -
2- Eine TIN der Triangulation
Wird vom GEOS Modul ausgeführt
Verfügbarkeit: 2.1.0
 Diese Funktion unterstützt 3d und lässt den Z-Index nicht fallen.
Diese Funktion unterstützt 3d und lässt den Z-Index nicht fallen.
 Diese Funktion unterstützt Dreiecke und dreieckige unregelmäßige Netzoberflächen (TIN).
Diese Funktion unterstützt Dreiecke und dreieckige unregelmäßige Netzoberflächen (TIN).
Beispiele
 Ursprüngliche Polygone our original geometry
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
) |
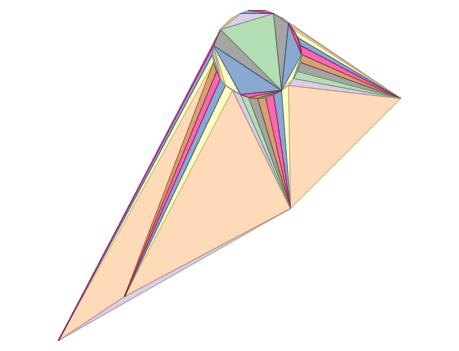
ST_DelaunayTriangles von 2 Polygonen: delaunay triangulierte Polygone, jedes der Dreiecke ist in einer eigenen Farbe dargestellt
geometries overlaid multilinestring triangles
SELECT
ST_DelaunayTriangles(
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
))
As dtriag;
|
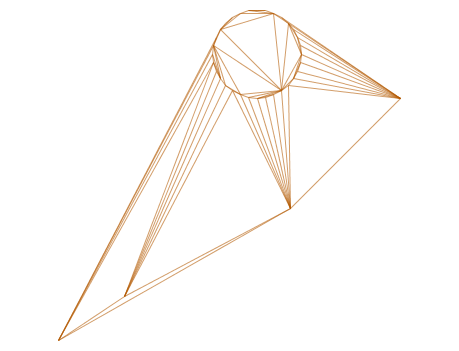
-- Delaunay-Dreiecke als MultiLinestring
SELECT
ST_DelaunayTriangles(
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
),0.001,1)
As dtriag;
|
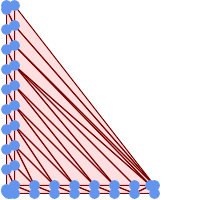
-- Delaunay Dreiecke von 45 Punkten als 55 Dreieckspolygone
this produces a table of 42 points that form an L shape SELECT (ST_DumpPoints(ST_GeomFromText( 'MULTIPOINT(14 14,34 14,54 14,74 14,94 14,114 14,134 14, 150 14,154 14,154 6,134 6,114 6,94 6,74 6,54 6,34 6, 14 6,10 6,8 6,7 7,6 8,6 10,6 30,6 50,6 70,6 90,6 110,6 130, 6 150,6 170,6 190,6 194,14 194,14 174,14 154,14 134,14 114, 14 94,14 74,14 54,14 34,14 14)'))).geom INTO TABLE l_shape; output as individual polygon triangles SELECT ST_AsText((ST_Dump(geom)).geom) As wkt FROM ( SELECT ST_DelaunayTriangles(ST_Collect(geom)) As geom FROM l_shape) As foo; wkt POLYGON((6 194,6 190,14 194,6 194)) POLYGON((14 194,6 190,14 174,14 194)) POLYGON((14 194,14 174,154 14,14 194)) POLYGON((154 14,14 174,14 154,154 14)) POLYGON((154 14,14 154,150 14,154 14)) POLYGON((154 14,150 14,154 6,154 14))
|
Beispiel mit Scheitelpunkten mit Z-Werten.
3D multipoint SELECT ST_AsText(ST_DelaunayTriangles(ST_GeomFromText( 'MULTIPOINT Z(14 14 10, 150 14 100,34 6 25, 20 10 150)'))) As wkt; wkt GEOMETRYCOLLECTION Z (POLYGON Z ((14 14 10,20 10 150,34 6 25,14 14 10)) ,POLYGON Z ((14 14 10,34 6 25,150 14 100,14 14 10)))