Name
ST_DelaunayTriangles — 返回几何体顶点的 Delaunay 三角剖分。
Synopsis
geometry ST_DelaunayTriangles(geometry g1, float tolerance = 0.0, int4 flags = 0);
描述
计算输入几何体顶点的 Delaunay 三角剖分。 可选的容差可用于将附近的输入顶点捕捉在一起,这在某些情况下提高了稳健性。 结果几何图形以输入顶点的凸包为边界。 结果几何表示由标志代码确定:
-
0- 三角形 POLYGON 的 GEOMETRYCOLLECTION(默认) -
1- 三角测量边缘的多线 -
2- 三角测量的 TIN
这个函数是由 GEOS 模块执行的。
可用性:2.1.0
 该函数支持 3d 并且不会丢失 z-index。
该函数支持 3d 并且不会丢失 z-index。
 此函数支持三角形和不规则三角网面 (TIN)。
此函数支持三角形和不规则三角网面 (TIN)。
示例
 原始多边形 our original geometry
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
) |
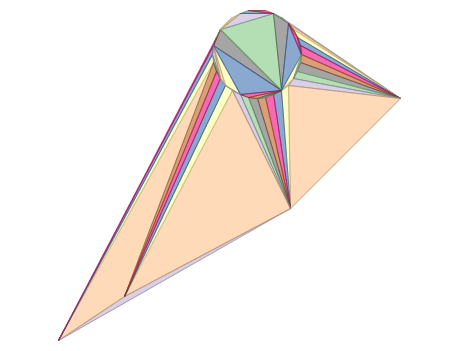
2 个多边形的 ST_DelaunayTriangles:delaunay 三角形多边形,每个三角形以不同颜色为主题
geometries overlaid multilinestring triangles
SELECT
ST_DelaunayTriangles(
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
))
As dtriag;
|
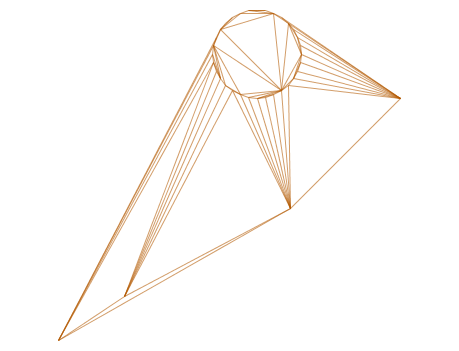
-- delaunay 三角形作为多线串
SELECT
ST_DelaunayTriangles(
ST_Union(ST_GeomFromText('POLYGON((175 150, 20 40,
50 60, 125 100, 175 150))'),
ST_Buffer(ST_GeomFromText('POINT(110 170)'), 20)
),0.001,1)
As dtriag;
|
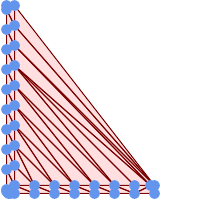
-- 45 个点的 delaunay 三角形作为 55 个三角形多边形
this produces a table of 42 points that form an L shape SELECT (ST_DumpPoints(ST_GeomFromText( 'MULTIPOINT(14 14,34 14,54 14,74 14,94 14,114 14,134 14, 150 14,154 14,154 6,134 6,114 6,94 6,74 6,54 6,34 6, 14 6,10 6,8 6,7 7,6 8,6 10,6 30,6 50,6 70,6 90,6 110,6 130, 6 150,6 170,6 190,6 194,14 194,14 174,14 154,14 134,14 114, 14 94,14 74,14 54,14 34,14 14)'))).geom INTO TABLE l_shape; output as individual polygon triangles SELECT ST_AsText((ST_Dump(geom)).geom) As wkt FROM ( SELECT ST_DelaunayTriangles(ST_Collect(geom)) As geom FROM l_shape) As foo; wkt POLYGON((6 194,6 190,14 194,6 194)) POLYGON((14 194,6 190,14 174,14 194)) POLYGON((14 194,14 174,154 14,14 194)) POLYGON((154 14,14 174,14 154,154 14)) POLYGON((154 14,14 154,150 14,154 14)) POLYGON((154 14,150 14,154 6,154 14))
|
使用具有 Z 值的顶点的示例。
3D multipoint SELECT ST_AsText(ST_DelaunayTriangles(ST_GeomFromText( 'MULTIPOINT Z(14 14 10, 150 14 100,34 6 25, 20 10 150)'))) As wkt; wkt GEOMETRYCOLLECTION Z (POLYGON Z ((14 14 10,20 10 150,34 6 25,14 14 10)) ,POLYGON Z ((14 14 10,34 6 25,150 14 100,14 14 10)))