Name
ST_Contains — 测试 B 的每个点是否都位于 A 中,并且它们的内部是否有一个共同点
Synopsis
boolean ST_Contains(geometry geomA, geometry geomB);
描述
如果几何图形 A 包含几何图形 B,则返回 TRUE。当且仅当 B 的所有点都位于 A 内部(即在 A 的内部或边界中)时,A 包含 B(或者等效地,B 中没有点位于 A 的外部),并且 A 和 B 的内部至少有一个共同点。
用数学术语来说: ST_Contains(A, B) ⇔ (A ⋂ B = B) ∧ (Int(A) ⋂ Int(B) ≠ ∅)
包含关系是自反的:每个几何图形都包含其自身。 (相反,在ST_ContainsProperly谓词中,几何图形未正确包含自身。)该关系是反对称的:如果 ST_Contains(A,B) = true 且 ST_Contains(B,A) = true,则两个几何图形必须在拓扑上相等 ( ST_Equals(A,B) = true)。
ST_Contains 与 ST_Within相反。 因此,ST_Contains(A,B) = ST_Within(B,A)。
![[Note]](../images/note.png)
|
|
|
因为内部必须有一个公共点,所以定义的一个微妙之处是多边形和线不包含完全位于其边界内的线和点。 有关更多详细信息,请参阅 OGC涵盖、包含、内部的微妙之处。 ST_Covers 谓词提供了更具包容性的关系。 |
![[Note]](../images/note.png)
|
|
|
此功能自动包括利用几何上可用的任何空间索引的边界框比较。 要避免使用索引,请使用函数 |
它是通过GEOS模块实现的
增强:2.3.0 PIP 短路(快速判断仅限于多边形和点)已得到增强,以支持具有更少点的多点。 以前的版本仅支持面和点组合。
![[Important]](../images/important.png)
|
|
|
增强:3.0.0 启用了对 |
![[Important]](../images/important.png)
|
|
|
请勿将此函数用于无效的几何图形。 你会得到意想不到的结果。 |
注意:这是返回布尔值而不是整数的“允许”版本。
 此方法实现了 SQL 1.1 的 OGC 简单功能规范。 s2.1.1.2 // s2.1.13.3 - 与内部相同(几何 B、几何 A)
此方法实现了 SQL 1.1 的 OGC 简单功能规范。 s2.1.1.2 // s2.1.13.3 - 与内部相同(几何 B、几何 A)
 该方法实现了SQL/MM规范。 SQL-MM 3: 5.1.31
该方法实现了SQL/MM规范。 SQL-MM 3: 5.1.31
示例
ST_Contains 在以下情况下返回 TRUE:

|
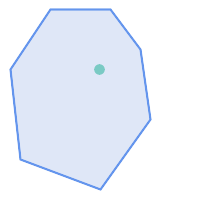
|
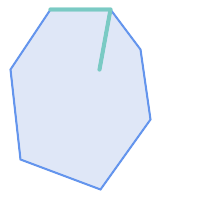
|
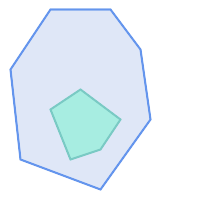
|
ST_Contains 在以下情况下返回 FALSE:
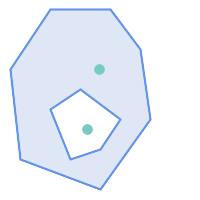
|

|
由于内部相交条件,ST_Contains 在以下情况下返回 FALSE(而 ST_Covers 返回 TRUE):

|
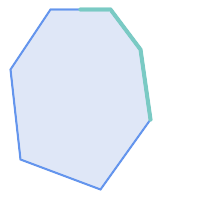
|
-- A circle within a circle
SELECT ST_Contains(smallc, bigc) As smallcontainsbig,
ST_Contains(bigc,smallc) As bigcontainssmall,
ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,
ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;
-- Result
smallcontainsbig | bigcontainssmall | bigcontainsunion | bigisunion | bigcoversexterior | bigcontainsexterior
------------------+------------------+------------------+------------+-------------------+---------------------
f | t | t | t | t | f
-- Example demonstrating difference between contains and contains properly
SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, ST_ContainsProperly(geomA, geomA) AS acontainspropa,
ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),
( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),
( ST_Point(1,1) )
) As foo(geomA);
geomtype | acontainsa | acontainspropa | acontainsba | acontainspropba
--------------+------------+----------------+-------------+-----------------
ST_Polygon | t | f | f | f
ST_LineString | t | f | f | f
ST_Point | t | t | f | f