gbox_geocentric_get_gbox_cartesian()

int gbox_geocentric_get_gbox_cartesian	(	const GBOX *	gbox_geocentric,
		GBOX *	gbox_planar
	)

Definition at line 3596 of file lwgeodetic.c.

{
        /* Normalized corners of the bounding volume */
        POINT3D corners[8];
        POINT3D cap_center = {0,0,0};
        double furthest_angle = 0.0;
        double cap_angle = 0.0;
        int all_longitudes = LW_FALSE;
        double lon0 = -M_PI, lon1 = M_PI;
        double lat0, lat1;
        GEOGRAPHIC_POINT cap_center_g;
 
        if (!gbox_geocentric || !gbox_planar)
        {
                lwerror("Null pointer passed to %s", __func__);
                return LW_FALSE;
        }
 
#define CORNER_SET(ii, xx, yy, zz) { \
        corners[ii].x = gbox_geocentric->xx; \
        corners[ii].y = gbox_geocentric->yy; \
        corners[ii].z = gbox_geocentric->zz; \
        }
 
        /*
        * First find a "centered" vector to serve as the mid-point
        * of the input bounding volume.
        */
        CORNER_SET(0, xmin, ymin, zmin);
        CORNER_SET(1, xmax, ymin, zmin);
        CORNER_SET(2, xmin, ymax, zmin);
        CORNER_SET(3, xmax, ymax, zmin);
        CORNER_SET(4, xmin, ymin, zmax);
        CORNER_SET(5, xmax, ymin, zmax);
        CORNER_SET(6, xmin, ymax, zmax);
        CORNER_SET(7, xmax, ymax, zmax);
 
        /*
        * Normalize the volume corners
        * and normalize the final vector.
        */
        for (uint32_t i = 0; i < 8; i++)
        {
                normalize(&(corners[i]));
                cap_center.x += corners[i].x;
                cap_center.y += corners[i].y;
                cap_center.z += corners[i].z;
        }
        normalize(&cap_center);
 
        /*
        * Find the volume corner that is furthest from the center,
        * and calculate the angle between the center and the corner.
        * Now we have a "cap" (center and angle)
        */
        for (uint32_t i = 0; i < 8; i++)
        {
                double angle = vector_angle(&cap_center, &(corners[i]));
                if (angle > furthest_angle)
                        furthest_angle = angle;
        }
        cap_angle = furthest_angle;
 
        /*
        * Calculate the planar box that contains the cap.
        * If the cap contains a pole, then we include all longitudes
        */
        cart2geog(&cap_center, &cap_center_g);
 
        /* Check whether cap includes the south pole */
        lat0 = cap_center_g.lat - cap_angle;
        if (lat0 <= -M_PI_2)
        {
                lat0 = -M_PI_2;
                all_longitudes = LW_TRUE;
        }
 
        /* Check whether cap includes the north pole */
        lat1 = cap_center_g.lat + cap_angle;
        if (lat1 >= M_PI_2)
        {
                lat1 = M_PI_2;
                all_longitudes = LW_TRUE;
        }
 
        if (!all_longitudes)
        {
                // Compute the range of longitudes covered by the cap.  We use the law
                // of sines for spherical triangles.  Consider the triangle ABC where
                // A is the north pole, B is the center of the cap, and C is the point
                // of tangency between the cap boundary and a line of longitude.  Then
                // C is a right angle, and letting a,b,c denote the sides opposite A,B,C,
                // we have sin(a)/sin(A) = sin(c)/sin(C), or sin(A) = sin(a)/sin(c).
                // Here "a" is the cap angle, and "c" is the colatitude (90 degrees
                // minus the latitude).  This formula also works for negative latitudes.
                //
                // The formula for sin(a) follows from the relationship h = 1 - cos(a).
 
                double sin_a = sin(cap_angle);
                double sin_c = cos(cap_center_g.lat);
                if (sin_a <= sin_c)
                {
                        double angle_A = asin(sin_a / sin_c);
                        lon0 = remainder(cap_center_g.lon - angle_A, 2 * M_PI);
                        lon1 = remainder(cap_center_g.lon + angle_A, 2 * M_PI);
                }
                else
                {
                        lon0 = -M_PI;
                        lon1 =  M_PI;
                }
        }
 
        gbox_planar->xmin = rad2deg(lon0);
        gbox_planar->ymin = rad2deg(lat0);
        gbox_planar->xmax = rad2deg(lon1);
        gbox_planar->ymax = rad2deg(lat1);
        FLAGS_SET_GEODETIC(gbox_planar->flags, 0);
        FLAGS_SET_Z(gbox_planar->flags, 0);
        FLAGS_SET_M(gbox_planar->flags, 0);
 
        return LW_TRUE;
}

References cart2geog(), CORNER_SET, GBOX::flags, FLAGS_SET_GEODETIC, FLAGS_SET_M, FLAGS_SET_Z, GEOGRAPHIC_POINT::lat, GEOGRAPHIC_POINT::lon, LW_FALSE, LW_TRUE, lwerror(), normalize(), rad2deg, vector_angle(), POINT3D::x, GBOX::xmax, GBOX::xmin, POINT3D::y, GBOX::ymax, GBOX::ymin, and POINT3D::z.

Referenced by BOX3D_BOXLL_TEST(), and gserialized_estimated_extent().

Here is the call graph for this function:

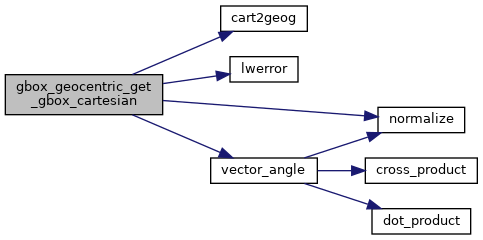
Here is the caller graph for this function: