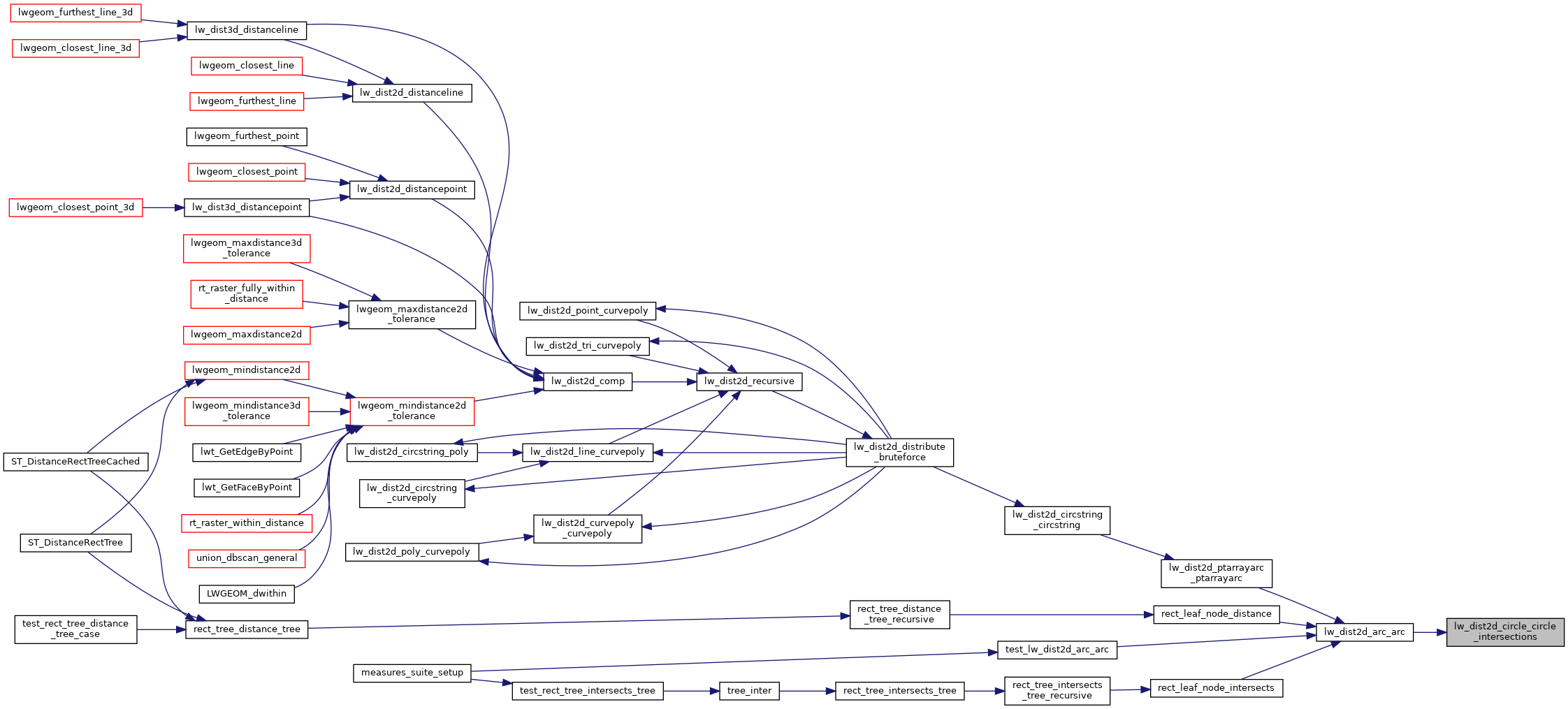
lw_dist2d_circle_circle_intersections()

static uint32_t lw_dist2d_circle_circle_intersections ( const POINT2D *  cA, double  rA, const POINT2D *  cB, double  rB, POINT2D *  I  )

static

Calculates the intersection points of two overlapping circles.

This function assumes the circles are known to intersect at one or two points. Specifically, the distance 'd' between their centers must satisfy: d < (rA + rB) and d > fabs(rA - rB) If these conditions are not met, the results are undefined.

Parameters

cA	[in] Pointer to the center point of the first circle (A).
rA	[in] The radius of the first circle (A).
cB	[in] Pointer to the center point of the second circle (B).
rB	[in] The radius of the second circle (B).
I	[out] Pointer to an array of at least 2 POINT2D structs to store the results. I[0] will contain the first intersection point. If a second exists, it will be in I[1].

Returns

int The number of intersection points found (1 or 2). Returns 0 if the centers are coincident or another error occurs.

Definition at line 1626 of file measures.c.

{
        // Vector from center A to center B
        double dx = cB->x - cA->x;
        double dy = cB->y - cA->y;
 
        // Distance between the centers
        double d = sqrt(dx * dx + dy * dy);
 
        // 'a' is the distance from the center of circle A to the point P,
        // which is the base of the right triangle formed by cA, P, and an intersection point.
        double a = (rA * rA - rB * rB + d * d) / (2.0 * d);
 
        // 'h' is the height of that right triangle.
        double h_squared = rA * rA - a * a;
 
        // Due to floating point errors, h_squared can be slightly negative.
        // This happens when the circles are perfectly tangent. Clamp to 0.
        if (h_squared < 0.0)
                h_squared = 0.0;
 
        double h = sqrt(h_squared);
 
        // Find the coordinates of point P
        double Px = cA->x + a * (dx / d);
        double Py = cA->y + a * (dy / d);
 
        // The two intersection points are found by moving from P by a distance 'h'
        // in directions perpendicular to the line connecting the centers.
        // The perpendicular vector to (dx, dy) is (-dy, dx).
 
        // Intersection point 1
        I[0].x = Px - h * (dy / d);
        I[0].y = Py + h * (dx / d);
 
        // If h is very close to 0, the circles are tangent and there's only one intersection point.
        if (FP_IS_ZERO(h))
                return 1;
 
        // Intersection point 2
        I[1].x = Px + h * (dy / d);
        I[1].y = Py - h * (dx / d);
 
        return 2;
}

References FP_IS_ZERO, POINT2D::x, and POINT2D::y.

Referenced by lw_dist2d_arc_arc().

Here is the caller graph for this function: