◆ gbox_geocentric_get_gbox_cartesian()
Definition at line 3596 of file lwgeodetic.c.
void cart2geog(const POINT3D *p, GEOGRAPHIC_POINT *g)
Convert cartesian coordinates on unit sphere to spherical coordinates.
Definition: lwgeodetic.c:414
#define CORNER_SET(ii, xx, yy, zz)
double vector_angle(const POINT3D *v1, const POINT3D *v2)
Angle between two unit vectors.
Definition: lwgeodetic.c:505
void void lwerror(const char *fmt,...) __attribute__((format(printf
Write a notice out to the error handler.
Definition: liblwgeom.h:401
References cart2geog(), CORNER_SET, GBOX::flags, FLAGS_SET_GEODETIC, FLAGS_SET_M, FLAGS_SET_Z, GEOGRAPHIC_POINT::lat, GEOGRAPHIC_POINT::lon, LW_FALSE, LW_TRUE, lwerror(), normalize(), rad2deg, vector_angle(), POINT3D::x, GBOX::xmax, GBOX::xmin, POINT3D::y, GBOX::ymax, GBOX::ymin, and POINT3D::z.
Referenced by BOX3D_BOXLL_TEST(), and gserialized_estimated_extent().
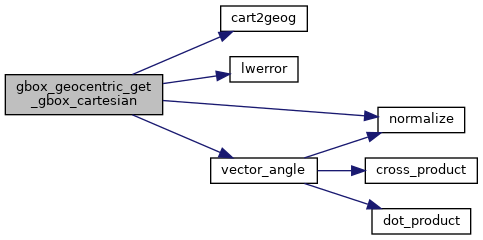
Here is the call graph for this function:
Here is the caller graph for this function:
