ptarray_distance_spheroid()

static double ptarray_distance_spheroid ( const POINTARRAY *  pa1, const POINTARRAY *  pa2, const SPHEROID *  s, double  tolerance, int  check_intersection  )

static

Definition at line 1841 of file lwgeodetic.c.

{
        GEOGRAPHIC_EDGE e1, e2;
        GEOGRAPHIC_POINT g1, g2;
        GEOGRAPHIC_POINT nearest1, nearest2;
        POINT3D A1, A2, B1, B2;
        const POINT2D *p;
        double distance;
        uint32_t i, j;
        int use_sphere = (s->a == s->b ? 1 : 0);
 
        /* Make result really big, so that everything will be smaller than it */
        distance = FLT_MAX;
 
        /* Empty point arrays? Return negative */
        if ( pa1->npoints == 0 || pa2->npoints == 0 )
                return -1.0;
 
        /* Handle point/point case here */
        if ( pa1->npoints == 1 && pa2->npoints == 1 )
        {
                p = getPoint2d_cp(pa1, 0);
                geographic_point_init(p->x, p->y, &g1);
                p = getPoint2d_cp(pa2, 0);
                geographic_point_init(p->x, p->y, &g2);
                /* Sphere special case, axes equal */
                distance = s->radius * sphere_distance(&g1, &g2);
                if ( use_sphere )
                        return distance;
                /* Below tolerance, actual distance isn't of interest */
                else if ( distance < 0.95 * tolerance )
                        return distance;
                /* Close or greater than tolerance, get the real answer to be sure */
                else
                        return spheroid_distance(&g1, &g2, s);
        }
 
        /* Handle point/line case here */
        if ( pa1->npoints == 1 || pa2->npoints == 1 )
        {
                /* Handle one/many case here */
                uint32_t i;
                const POINTARRAY *pa_one;
                const POINTARRAY *pa_many;
 
                if ( pa1->npoints == 1 )
                {
                        pa_one = pa1;
                        pa_many = pa2;
                }
                else
                {
                        pa_one = pa2;
                        pa_many = pa1;
                }
 
                /* Initialize our point */
                p = getPoint2d_cp(pa_one, 0);
                geographic_point_init(p->x, p->y, &g1);
 
                /* Initialize start of line */
                p = getPoint2d_cp(pa_many, 0);
                geographic_point_init(p->x, p->y, &(e1.start));
 
                /* Iterate through the edges in our line */
                for ( i = 1; i < pa_many->npoints; i++ )
                {
                        double d;
                        p = getPoint2d_cp(pa_many, i);
                        geographic_point_init(p->x, p->y, &(e1.end));
                        /* Get the spherical distance between point and edge */
                        d = s->radius * edge_distance_to_point(&e1, &g1, &g2);
                        /* New shortest distance! Record this distance / location */
                        if ( d < distance )
                        {
                                distance = d;
                                nearest2 = g2;
                        }
                        /* We've gotten closer than the tolerance... */
                        if ( d <= tolerance )
                        {
                                /* Working on a sphere? The answer is correct, return */
                                if ( use_sphere )
                                {
                                        return d;
                                }
                                /* Far enough past the tolerance that the spheroid calculation won't change things */
                                else if ( d <= tolerance * 0.95 )
                                {
                                        return d;
                                }
                                /* On a spheroid and near the tolerance? Confirm that we are *actually* closer than tolerance */
                                else
                                {
                                        d = spheroid_distance(&g1, &nearest2, s);
                                        /* Yes, closer than tolerance, return! */
                                        if ( d <= tolerance )
                                                return d;
                                }
                        }
                        e1.start = e1.end;
                }
 
                /* On sphere, return answer */
                if ( use_sphere )
                        return distance;
                /* On spheroid, calculate final answer based on closest approach */
                else
                        return spheroid_distance(&g1, &nearest2, s);
 
        }
 
        /* Initialize start of line 1 */
        p = getPoint2d_cp(pa1, 0);
        geographic_point_init(p->x, p->y, &(e1.start));
        geog2cart(&(e1.start), &A1);
 
 
        /* Handle line/line case */
        for ( i = 1; i < pa1->npoints; i++ )
        {
                p = getPoint2d_cp(pa1, i);
                geographic_point_init(p->x, p->y, &(e1.end));
                geog2cart(&(e1.end), &A2);
 
                /* Initialize start of line 2 */
                p = getPoint2d_cp(pa2, 0);
                geographic_point_init(p->x, p->y, &(e2.start));
                geog2cart(&(e2.start), &B1);
 
                for ( j = 1; j < pa2->npoints; j++ )
                {
                        double d;
 
                        p = getPoint2d_cp(pa2, j);
                        geographic_point_init(p->x, p->y, &(e2.end));
                        geog2cart(&(e2.end), &B2);
 
                        LWDEBUGF(4, "e1.start == GPOINT(%.6g %.6g) ", e1.start.lat, e1.start.lon);
                        LWDEBUGF(4, "e1.end == GPOINT(%.6g %.6g) ", e1.end.lat, e1.end.lon);
                        LWDEBUGF(4, "e2.start == GPOINT(%.6g %.6g) ", e2.start.lat, e2.start.lon);
                        LWDEBUGF(4, "e2.end == GPOINT(%.6g %.6g) ", e2.end.lat, e2.end.lon);
 
                        if ( check_intersection && edge_intersects(&A1, &A2, &B1, &B2) )
                        {
                                LWDEBUG(4,"edge intersection! returning 0.0");
                                return 0.0;
                        }
                        d = s->radius * edge_distance_to_edge(&e1, &e2, &g1, &g2);
                        LWDEBUGF(4,"got edge_distance_to_edge %.8g", d);
 
                        if ( d < distance )
                        {
                                distance = d;
                                nearest1 = g1;
                                nearest2 = g2;
                        }
                        if ( d <= tolerance )
                        {
                                if ( use_sphere )
                                {
                                        return d;
                                }
                                else
                                {
                                        d = spheroid_distance(&nearest1, &nearest2, s);
                                        if ( d <= tolerance )
                                                return d;
                                }
                        }
 
                        /* Copy end to start to allow a new end value in next iteration */
                        e2.start = e2.end;
                        B1 = B2;
                }
 
                /* Copy end to start to allow a new end value in next iteration */
                e1.start = e1.end;
                A1 = A2;
                LW_ON_INTERRUPT(return -1.0);
        }
        LWDEBUGF(4,"finished all loops, returning %.8g", distance);
 
        if ( use_sphere )
                return distance;
        else
                return spheroid_distance(&nearest1, &nearest2, s);
}

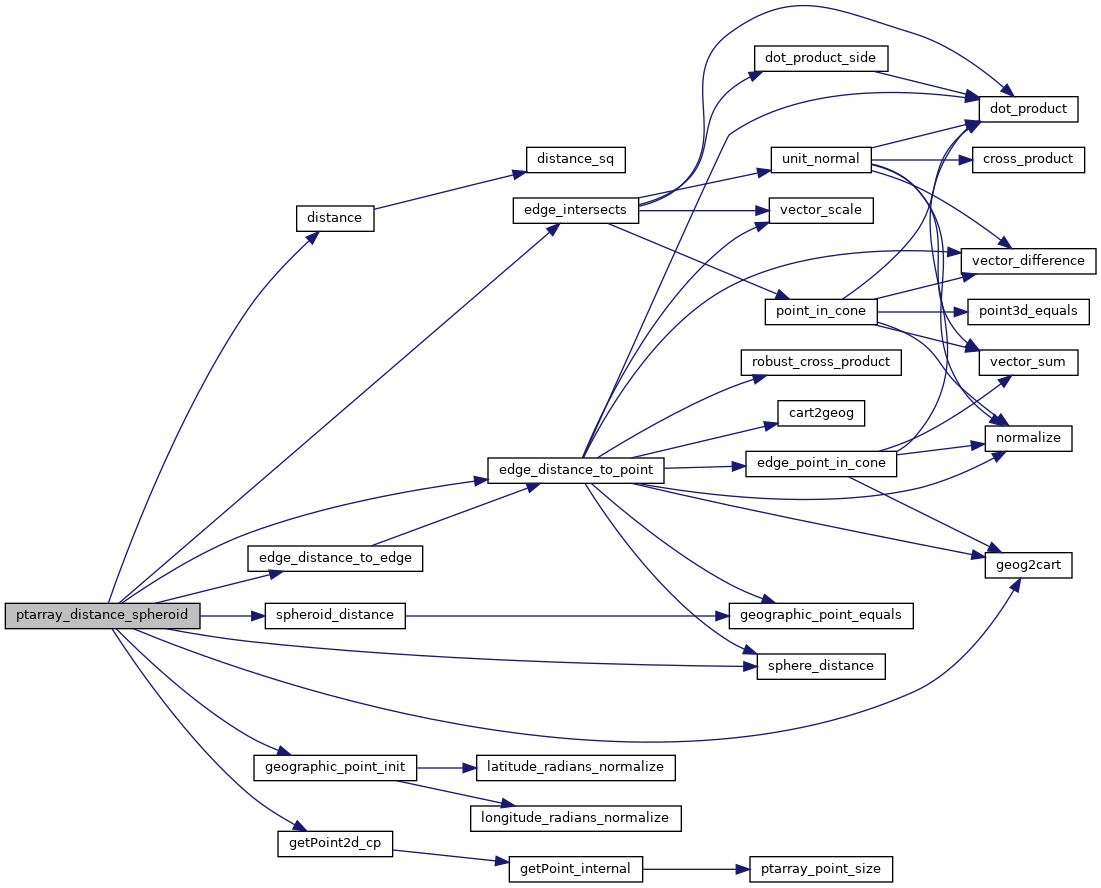
References distance(), edge_distance_to_edge(), edge_distance_to_point(), edge_intersects(), GEOGRAPHIC_EDGE::end, geog2cart(), geographic_point_init(), getPoint2d_cp(), GEOGRAPHIC_POINT::lat, GEOGRAPHIC_POINT::lon, LW_ON_INTERRUPT, LWDEBUG, LWDEBUGF, POINTARRAY::npoints, s, sphere_distance(), spheroid_distance(), GEOGRAPHIC_EDGE::start, POINT2D::x, and POINT2D::y.

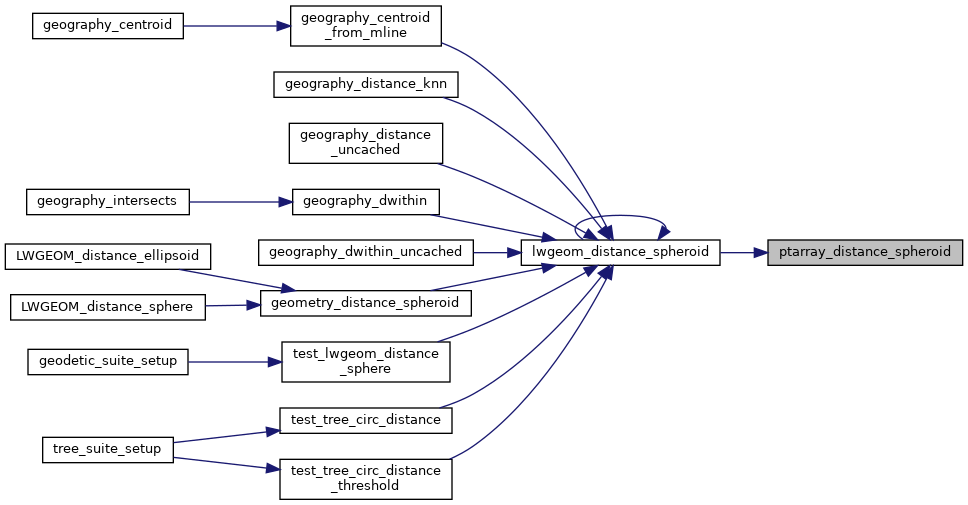
Referenced by lwgeom_distance_spheroid().

Here is the call graph for this function:

Here is the caller graph for this function: