sphere_project()

int sphere_project	(	const GEOGRAPHIC_POINT *	r,
		double	distance,
		double	azimuth,
		GEOGRAPHIC_POINT *	n
	)

Given a starting location r, a distance and an azimuth to the new point, compute the location of the projected point on the unit sphere.

Definition at line 1320 of file lwgeodetic.c.

{
        double d = distance;
        double lat1 = r->lat;
        double lon1 = r->lon;
        double lat2, lon2;
 
        lat2 = asin(sin(lat1)*cos(d) + cos(lat1)*sin(d)*cos(azimuth));
 
        /* If we're going straight up or straight down, we don't need to calculate the longitude */
        /* TODO: this isn't quite true, what if we're going over the pole? */
        if ( FP_EQUALS(azimuth, M_PI) || FP_EQUALS(azimuth, 0.0) )
        {
                lon2 = r->lon;
        }
        else
        {
                lon2 = lon1 + atan2(sin(azimuth)*sin(d)*cos(lat1), cos(d)-sin(lat1)*sin(lat2));
        }
 
        if ( isnan(lat2) || isnan(lon2) )
                return LW_FAILURE;
 
        n->lat = lat2;
        n->lon = lon2;
 
        return LW_SUCCESS;
}

References distance(), FP_EQUALS, GEOGRAPHIC_POINT::lat, GEOGRAPHIC_POINT::lon, LW_FAILURE, LW_SUCCESS, and r.

Referenced by circ_center_spherical(), interpolate_point4d_spheroid(), and test_sphere_project().

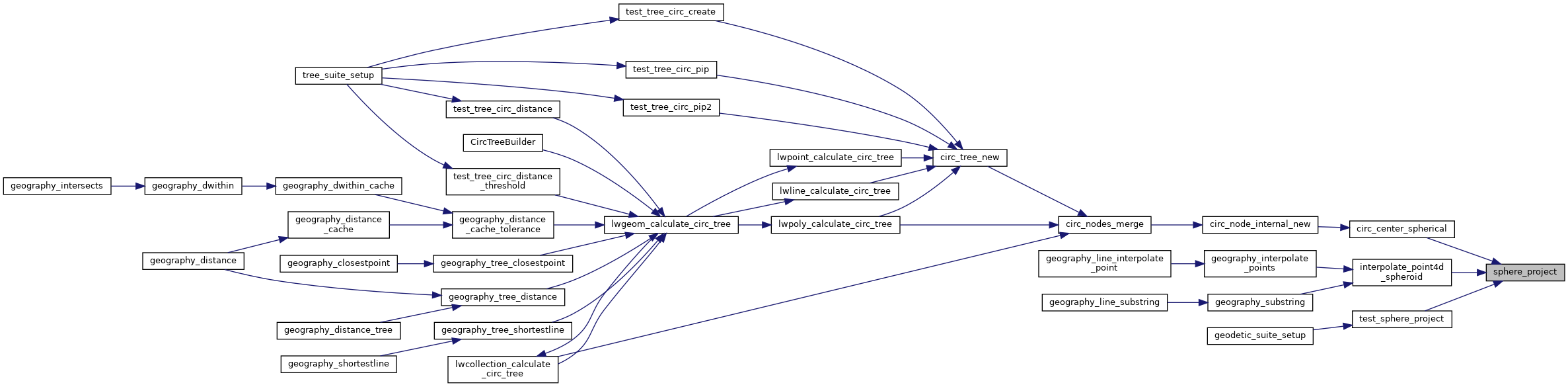
Here is the call graph for this function:

Here is the caller graph for this function: