Name
ST_LargestEmptyCircle — Computes the largest circle not overlapping a geometry.
Synopsis
(geometry, geometry, double precision) ST_LargestEmptyCircle(geometry geom, double precision tolerance=0.0, geometry boundary=POINT EMPTY);
Descripción
Finds the largest circle which does not overlap a set of point and line obstacles. (Polygonal geometries may be included as obstacles, but only their boundary lines are used.) The center of the circle is constrained to lie inside a polygonal boundary, which by default is the convex hull of the input geometry. The circle center is the point in the interior of the boundary which has the farthest distance from the obstacles. The circle itself is provided by the center point and a nearest point lying on an obstacle determining the circle radius.
The circle center is determined to a given accuracy specified by a distance tolerance, using an iterative algorithm. If the accuracy distance is not specified a reasonable default is used.
Returns a record with fields:
-
center- center point of the circle -
nearest- a point on the geometry nearest to the center -
radius- radius of the circle
To find the largest empty circle in the interior of a polygon, see ST_MaximumInscribedCircle.
Availability: 3.4.0.
Requires GEOS >= 3.9.0.
Ejemplos
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
'MULTILINESTRING (
(10 100, 60 180, 130 150, 190 160),
(20 50, 70 70, 90 20, 110 40),
(160 30, 100 100, 180 100))');
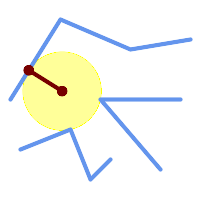
Largest Empty Circle within a set of lines.
SELECT radius,
center,
nearest
FROM ST_LargestEmptyCircle(
ST_Collect(
'MULTIPOINT ((70 50), (60 130), (130 150), (80 90))'::geometry,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry),
0,
'POLYGON ((90 190, 10 100, 60 10, 190 40, 120 100, 190 180, 90 190))'::geometry
);
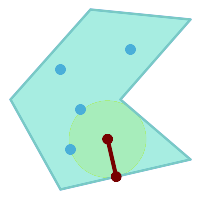
Largest Empty Circle within a set of points, constrained to lie in a polygon. The constraint polygon boundary must be included as an obstacle, as well as specified as the constraint for the circle center.